| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 12 Linear Programming
Welcome to this essential resource providing comprehensive solutions for the Class 12 NCERT Exemplar problems dedicated to Linear Programming Problems (LPPs). This chapter introduces a powerful mathematical technique used for optimizing outcomes (like maximizing profit or minimizing cost) subject to various limitations or constraints, finding wide application in fields like business management, operations research, economics, and logistics. The NCERT Exemplar questions significantly elevate the complexity beyond standard textbook exercises, challenging students with intricate problem formulations, graphical solutions involving potentially tricky feasible regions or constraints, and requiring a nuanced analysis of different types of possible solutions (or lack thereof). A strong grasp of LPP formulation and graphical solving techniques is crucial for developing practical problem-solving and decision-making skills.
A fundamental aspect, thoroughly addressed in these solutions, is the Formulation of LPPs. This involves the critical skill of translating often complex, real-world descriptive problems into a precise mathematical model. This process typically involves:
- Identifying the decision variables (usually denoted by $x, y$, representing quantities to be determined).
- Defining a linear objective function ($Z = ax + by + \dots$), which represents the quantity to be optimized (maximized or minimized, e.g., profit in $\textsf{₹}$ or cost).
- Establishing a set of linear constraints, expressed as inequalities ($\le, \ge$) or equalities (=), based on the limitations described in the problem (e.g., resource availability, production capacity, dietary requirements). Non-negativity constraints ($x \ge 0, y \ge 0$) are usually implicit.
For LPPs involving two decision variables, the primary solution method explored is the Graphical Method. These solutions meticulously demonstrate each step involved in this visual approach to finding the optimal solution:
- Graphing Constraints: Accurately plotting the straight lines corresponding to each linear constraint (treating inequalities as equalities for the boundary line). Attention must be paid to whether the line itself is included (for $\le, \ge$) or excluded (for $<, >$) from the solution space.
- Identifying the Feasible Region: Determining the common area (region) in the coordinate plane that simultaneously satisfies all the given constraints, including non-negativity. This requires shading the appropriate side of each constraint line. Exemplar problems might result in complex polygonal regions, potentially unbounded regions extending infinitely in one or more directions, or even an empty region if constraints are contradictory.
- Finding Corner Points: Precisely calculating the coordinates of the vertices (corner points) of the feasible region. This involves solving systems of linear equations for the intersecting boundary lines that form each vertex. Accuracy in these calculations is paramount.
- Evaluating the Objective Function: Substituting the coordinates of each corner point of the feasible region into the objective function $Z$ to find its value at each vertex.
- Determining the Optimal Solution: Based on the Fundamental Theorem of Linear Programming (which states that the optimal solution, if it exists, occurs at a corner point), identifying the maximum or minimum value of $Z$ among the values calculated at the corner points, and stating the corresponding values of the decision variables ($x, y$).
Crucially, the Exemplar often tests the understanding of Special Cases that can arise in LPPs. The solutions provide clear explanations and graphical identification methods for:
- Multiple Optimal Solutions: This occurs when the objective function has the same optimal value at more than one corner point. Graphically, this happens when the objective function line ($ax+by=k$) is parallel to one of the boundary lines forming an edge of the feasible region that contains optimal points. All points on that line segment then constitute optimal solutions.
- Unbounded Feasible Region: When the feasible region extends indefinitely. In such cases, the objective function might also be unbounded (no maximum for maximization problems, no minimum for minimization problems). The solutions demonstrate the necessary check: graph the objective function line for a value $k$ and see if it can be moved parallel to itself indefinitely within the feasible region to improve the objective value. If not, an optimal solution might still exist at a corner point.
- Infeasible Problems: Situations where the constraints are mutually contradictory, resulting in an empty feasible region. Graphically, there is no common shaded area satisfying all inequalities. Such problems have no solution.
By providing clear graphical representations, systematic procedures for identifying feasible regions and corner points, careful evaluation of the objective function, and correct interpretation of bounded, unbounded, and infeasible cases across various question formats, this resource aims to strengthen your proficiency in solving practical optimization problems using Linear Programming.
Solved Examples
Example 1 to 4 (Short Answer Type Questions)
Example 1: Determine the maximum value of Z = 4x + 3y if the feasible region for an LPP is shown in Fig. 12.1.
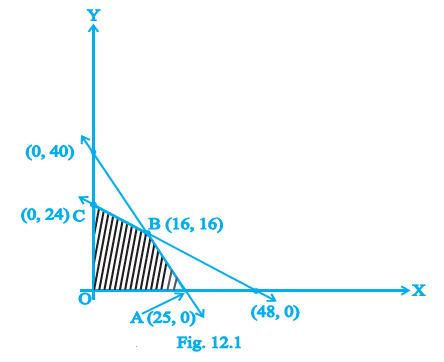
Answer:
According to the Fundamental Theorem of Linear Programming, the optimal solution (maximum or minimum) for a linear programming problem, if it exists, will occur at a corner point (vertex) of the feasible region.
From the given figure, the feasible region is the polygon OABC. The corner points (vertices) of this feasible region are:
- O = (0, 0)
- A = (25, 0)
- B = (15, 15)
- C = (0, 20)
The objective function is given by $Z = 4x + 3y$. We need to evaluate the value of Z at each of the corner points.
Evaluating Z at the corner points:
At O (0, 0): $Z = 4(0) + 3(0) = 0$
At A (25, 0): $Z = 4(25) + 3(0) = 100 + 0 = 100$
At B (15, 15): $Z = 4(15) + 3(15) = 60 + 45 = 105$
At C (0, 20): $Z = 4(0) + 3(20) = 0 + 60 = 60$
We can summarize the values of Z in a table:
| Corner Point (x, y) | Value of $Z = 4x + 3y$ |
| (0, 0) | 0 |
| (25, 0) | 100 |
| (15, 15) | 105 |
| (0, 20) | 60 |
Comparing the values of Z obtained at the corner points, we find that the maximum value is 105.
The maximum value of the objective function $Z = 4x + 3y$ is $\mathbf{105}$, and it occurs at the corner point (15, 15).
Example 2: Determine the minimum value of Z = 3x + 2y (if any), if the feasible region for an LPP is shown in Fig.12.2.
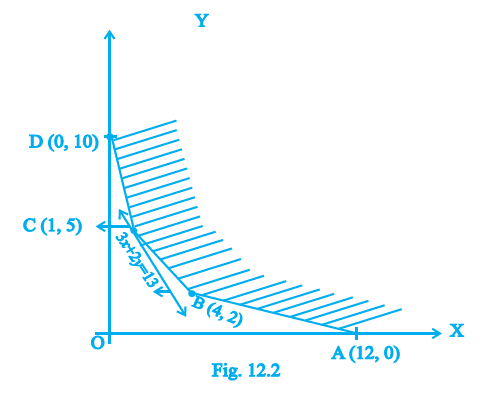
Answer:
The feasible region is given in the figure. It is an unbounded region.
The corner points (vertices) of the feasible region are the points where the boundary lines intersect. From the figure, the corner points are:
- A = (0, 10)
- B = (5, 5)
- C = (15, 0)
The objective function is given by $Z = 3x + 2y$. We need to evaluate the value of Z at each of the corner points.
Evaluating Z at the corner points:
At A (0, 10): $Z = 3(0) + 2(10) = 0 + 20 = 20$
At B (5, 5): $Z = 3(5) + 2(5) = 15 + 10 = 25$
At C (15, 0): $Z = 3(15) + 2(0) = 45 + 0 = 45$
We can summarize the values of Z in a table:
| Corner Point (x, y) | Value of $Z = 3x + 2y$ |
| (0, 10) | 20 |
| (5, 5) | 25 |
| (15, 0) | 45 |
The minimum value of Z at the corner points is 20, which occurs at (0, 10).
Since the feasible region is unbounded, we need to check if the minimum value of Z exists.
Consider the inequality $3x + 2y < 20$. We draw the graph of the line $3x + 2y = 20$. This line passes through (0, 10) and $(20/3, 0)$.
The open half-plane represented by $3x + 2y < 20$ is the region below the line $3x + 2y = 20$.
We need to determine if this open half-plane $3x + 2y < 20$ has any point in common with the feasible region.
Observing the figure, the feasible region is above the lines segment connecting (0,10), (5,5), and (15,0). The line $3x + 2y = 20$ passes through the point (0, 10).
Consider any point $(x, y)$ in the feasible region. The feasible region is defined by the constraints whose boundary lines pass through (0,10), (5,5), and (15,0). These lines are $x+y=10$ (through (0,10) and (5,5)) and $x+2y=15$ (through (5,5) and (15,0)), along with $x \ge 0$ and $y \ge 0$. The feasible region satisfies $x+y \ge 10$ and $x+2y \ge 15$.
For any point $(x, y)$ in the feasible region, we have $x \ge 0, y \ge 0, x+y \ge 10$, and $x+2y \ge 15$.
If we take a point $(x,y)$ in the feasible region other than (0,10), either $x > 0$ or $y > 10$ or both conditions might apply, subject to the constraints.
Consider the line $3x+2y=20$. This line passes through the corner point (0,10). All other points in the feasible region lie such that $3x+2y \ge 20$. This is because the feasible region lies "above" the line $3x+2y=20$ at points other than (0,10) which is on the line.
For example, consider point (5,5). $3(5)+2(5)=25 > 20$. Consider point (15,0). $3(15)+2(0)=45 > 20$.
Since the open half-plane $3x + 2y < 20$ does not contain any point of the feasible region, the minimum value of Z exists and is equal to the minimum value at the corner point (0, 10).
Therefore, the minimum value of the objective function $Z = 3x + 2y$ is $\mathbf{20}$, and it occurs at the corner point (0, 10).
Example 3: Solve the following LPP graphically:
Maximise Z = 2x + 3y,
subject to x + y ≤ 4, x ≥ 0, y ≥ 0
Answer:
The given Linear Programming Problem is:
Maximise $Z = 2x + 3y$
Subject to the constraints:
$x + y \le 4$
$x \ge 0$
$y \ge 0$
To find the feasible region, we first graph the boundary lines of the constraints.
- For $x+y \le 4$, the boundary line is $x+y = 4$. We find two points on this line:
- If $x = 0$, then $0 + y = 4 \implies y = 4$. Point is (0, 4).
- If $y = 0$, then $x + 0 = 4 \implies x = 4$. Point is (4, 0).
- For $x \ge 0$, this represents the region on or to the right of the y-axis.
- For $y \ge 0$, this represents the region on or above the x-axis.
The feasible region is the intersection of these three regions. It is the region in the first quadrant ($x \ge 0, y \ge 0$) below or on the line $x+y=4$. This forms a triangular region.
The corner points (vertices) of the feasible region are the points of intersection of the boundary lines. These are:
- Intersection of $x=0$ and $y=0$: (0, 0)
- Intersection of $x=0$ and $x+y=4$: Substitute $x=0$ into $x+y=4 \implies 0+y=4 \implies y=4$. Point is (0, 4).
- Intersection of $y=0$ and $x+y=4$: Substitute $y=0$ into $x+y=4 \implies x+0=4 \implies x=4$. Point is (4, 0).
The corner points are (0, 0), (0, 4), and (4, 0).
Now we evaluate the objective function $Z = 2x + 3y$ at each corner point to find the maximum value.
At corner point (0, 0):
$Z = 2(0) + 3(0) = 0$
At corner point (0, 4):
$Z = 2(0) + 3(4) = 0 + 12 = 12$
At corner point (4, 0):
$Z = 2(4) + 3(0) = 8 + 0 = 8$
We can list the values of Z at the corner points in a table:
| Corner Point (x, y) | Value of $Z = 2x + 3y$ |
| (0, 0) | 0 |
| (0, 4) | 12 |
| (4, 0) | 8 |
Comparing the values of Z, the maximum value is 12.
Therefore, the maximum value of $Z = 2x + 3y$ is $\mathbf{12}$, which occurs at the point (0, 4).
Example 4: A manufacturing company makes two types of television sets; one is black and white and the other is colour. The company has resources to make at most 300 sets a week. It takes Rs 1800 to make a black and white set and Rs 2700 to make a coloured set. The company can spend not more than Rs 648000 a week to make television sets. If it makes a profit of Rs 510 per black and white set and Rs 675 per coloured set, how many sets of each type should be produced so that the company has maximum profit? Formulate this problem as a LPP given that the objective is to maximise the profit.
Answer:
Let us formulate the given problem as a Linear Programming Problem.
Decision Variables:
Let $x$ be the number of black and white television sets produced per week.
Let $y$ be the number of coloured television sets produced per week.
Objective Function (Maximise Profit):
The profit from one black and white set is $\textsf{₹} 510$.
The profit from one coloured set is $\textsf{₹} 675$.
Total profit, $Z$, is the sum of profits from both types of sets.
$Z = 510x + 675y$
We want to maximise $Z$.
Constraints:
1. Resource Constraint (Maximum number of sets):
The total number of sets produced per week cannot exceed 300.
So, $x + y \le 300$.
2. Budget Constraint (Maximum expenditure):
The cost of making one black and white set is $\textsf{₹} 1800$.
The cost of making one coloured set is $\textsf{₹} 2700$.
The total weekly expenditure cannot exceed $\textsf{₹} 648000$.
So, the total cost is $1800x + 2700y$.
Thus, $1800x + 2700y \le 648000$.
We can simplify this inequality by dividing by 900:
$\frac{\cancel{1800}^{2}x}{\cancel{900}} + \frac{\cancel{2700}^{3}y}{\cancel{900}} \le \frac{\cancel{648000}^{720}}{\cancel{900}}$
$2x + 3y \le 720$.
3. Non-negativity Constraints:
The number of television sets produced cannot be negative.
So, $x \ge 0$ and $y \ge 0$.
Formulation of the LPP:
Maximise $Z = 510x + 675y$
Subject to the constraints:
$x + y \le 300$
$2x + 3y \le 720$
$x \ge 0$
$y \ge 0$
Example 5 to 6 (Long Answer Type Questions)
Example 5: Refer to Example 4. Solve the LPP.
Answer:
From Example 4, the Linear Programming Problem formulation is:
Maximise $Z = 510x + 675y$
Subject to:
$x + y \le 300$
$2x + 3y \le 720$
$x \ge 0$
$y \ge 0$
where $x$ is the number of black and white television sets and $y$ is the number of coloured television sets.
To solve this LPP graphically, we first determine the feasible region defined by the constraints.
We draw the boundary lines for each inequality:
- Line 1: $x + y = 300$
- If $x=0$, $y=300$. Point (0, 300).
- If $y=0$, $x=300$. Point (300, 0).
- Line 2: $2x + 3y = 720$
- If $x=0$, $3y=720 \implies y=240$. Point (0, 240).
- If $y=0$, $2x=720 \implies x=360$. Point (360, 0).
- $x \ge 0$: The region on or to the right of the y-axis.
- $y \ge 0$: The region on or above the x-axis.
The feasible region is the intersection of the regions satisfying all the constraints. It is a bounded region in the first quadrant.
The corner points (vertices) of the feasible region are the points of intersection of the boundary lines:
- Intersection of $x=0$ and $y=0$: (0, 0)
- Intersection of $y=0$ and $x+y=300$: Substitute $y=0$ into $x+y=300 \implies x+0=300 \implies x=300$. Point: (300, 0). (This point satisfies $2x+3y \le 720$ as $2(300)+3(0) = 600 \le 720$).
- Intersection of $x=0$ and $2x+3y=720$: Substitute $x=0$ into $2x+3y=720 \implies 2(0)+3y=720 \implies 3y=720 \implies y=240$. Point: (0, 240). (This point satisfies $x+y \le 300$ as $0+240 = 240 \le 300$).
- Intersection of $x+y=300$ and $2x+3y=720$:
From $x+y=300$, we get $y = 300 - x$. Substitute this into the second equation:
$2x + 3(300 - x) = 720$
$2x + 900 - 3x = 720$
$-x = 720 - 900$
$-x = -180$
$x = 180$
Now substitute $x=180$ back into $y = 300 - x$:
$y = 300 - 180 = 120$
Point: (180, 120). (This point satisfies $x \ge 0$ and $y \ge 0$ as $180 \ge 0$ and $120 \ge 0$).
The corner points of the feasible region are O(0, 0), A(300, 0), B(180, 120), and C(0, 240).
Next, we evaluate the objective function $Z = 510x + 675y$ at each corner point.
- At O (0, 0):
$Z = 510(0) + 675(0) = 0$
- At A (300, 0):
$Z = 510(300) + 675(0) = 153000 + 0 = 153000$
- At B (180, 120):
$Z = 510(180) + 675(120)$
$Z = 91800 + 81000 = 172800$
- At C (0, 240):
$Z = 510(0) + 675(240)$
$Z = 0 + 162000 = 162000$
We list the values of Z in the following table:
| Corner Point (x, y) | Value of $Z = 510x + 675y$ |
| (0, 0) | 0 |
| (300, 0) | 153000 |
| (180, 120) | 172800 |
| (0, 240) | 162000 |
Comparing the values of Z, the maximum value is 172800.
The maximum profit of $\textsf{₹} 172800$ is attained when $x = 180$ and $y = 120$.
Therefore, the company should produce 180 black and white television sets and 120 coloured television sets to achieve the maximum profit.
Example 6: Minimise Z = 3x + 5y subject to the constraints :
x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x , y ≥ 0
Answer:
The given Linear Programming Problem is:
Minimise $Z = 3x + 5y$
Subject to the constraints:
$x + 2y \ge 10$
$x + y \ge 6$
$3x + y \ge 8$
$x \ge 0, y \ge 0$
To find the feasible region, we graph the boundary lines corresponding to the inequality constraints:
- Line 1: $x + 2y = 10$
- If $x = 0$, $2y = 10 \implies y = 5$. Point: (0, 5).
- If $y = 0$, $x = 10$. Point: (10, 0).
- Line 2: $x + y = 6$
- If $x = 0$, $y = 6$. Point: (0, 6).
- If $y = 0$, $x = 6$. Point: (6, 0).
- Line 3: $3x + y = 8$
- If $x = 0$, $y = 8$. Point: (0, 8).
- If $y = 0$, $3x = 8 \implies x = 8/3$. Point: (8/3, 0).
- $x \ge 0, y \ge 0$: This restricts the feasible region to the first quadrant.
The feasible region is the intersection of these half-planes in the first quadrant. Graphing these lines and inequalities shows that the feasible region is an unbounded region.
The corner points (vertices) of the feasible region are the points where the boundary lines intersect and satisfy all constraints. We find the intersection points:
- Intersection of $x = 0$ and $3x + y = 8$: Substitute $x=0$ into $3x+y=8 \implies 3(0)+y=8 \implies y=8$. Point (0, 8). Check with $x+2y \ge 10$: $0+2(8)=16 \ge 10$ (True). Check with $x+y \ge 6$: $0+8=8 \ge 6$ (True). This is a corner point.
- Intersection of $3x + y = 8$ and $x + y = 6$: Subtract $x+y=6$ from $3x+y=8$: $(3x+y) - (x+y) = 8 - 6$ $2x = 2 \implies x = 1$. Substitute $x=1$ into $x+y=6$: $1+y=6 \implies y=5$. Point (1, 5). Check with $x+2y \ge 10$: $1+2(5)=1+10=11 \ge 10$ (True). This is a corner point.
- Intersection of $x + y = 6$ and $x + 2y = 10$: Subtract $x+y=6$ from $x+2y=10$: $(x+2y) - (x+y) = 10 - 6$ $y = 4$. Substitute $y=4$ into $x+y=6$: $x+4=6 \implies x=2$. Point (2, 4). Check with $3x+y \ge 8$: $3(2)+4=6+4=10 \ge 8$ (True). This is a corner point.
- Intersection of $x + 2y = 10$ and $y = 0$: Substitute $y=0$ into $x+2y=10 \implies x+2(0)=10 \implies x=10$. Point (10, 0). Check with $x+y \ge 6$: $10+0=10 \ge 6$ (True). Check with $3x+y \ge 8$: $3(10)+0=30 \ge 8$ (True). This is a corner point.
The corner points of the feasible region are (0, 8), (1, 5), (2, 4), and (10, 0).
Now, we evaluate the objective function $Z = 3x + 5y$ at each corner point:
- At (0, 8): $Z = 3(0) + 5(8) = 0 + 40 = 40$.
- At (1, 5): $Z = 3(1) + 5(5) = 3 + 25 = 28$.
- At (2, 4): $Z = 3(2) + 5(4) = 6 + 20 = 26$.
- At (10, 0): $Z = 3(10) + 5(0) = 30 + 0 = 30$.
We can list these values in a table:
| Corner Point (x, y) | Value of $Z = 3x + 5y$ |
| (0, 8) | 40 |
| (1, 5) | 28 |
| (2, 4) | 26 |
| (10, 0) | 30 |
The minimum value of Z at the corner points is 26, which occurs at the point (2, 4).
Since the feasible region is unbounded, we need to check if this minimum value is the actual minimum.
Consider the inequality $3x + 5y < 26$. This represents an open half-plane. We draw the line $3x + 5y = 26$. This line passes through the point (2, 4).
We need to check if the open half-plane $3x + 5y < 26$ has any point in common with the feasible region.
Since all the corner points (0, 8), (1, 5), (2, 4), (10, 0) give values of Z which are 26 or greater than 26, and the feasible region lies above or to the right of the boundary lines, the region $3x + 5y < 26$ does not overlap with the feasible region.
Therefore, the minimum value of $Z = 3x + 5y$ exists and is equal to the smallest value found at the corner points.
The minimum value of Z is $\mathbf{26}$, which occurs at the point (2, 4).
Example 7 to 8 (Multiple Choice Questions)
Choose the correct answer from the given four options in each of the Examples 7 to 8.
Example 7: The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20).Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is
(A) p = q
(B) p = 2q
(C) q = 2p
(D) q = 3p
Answer:
The given corner points of the feasible region are (0, 10), (5, 5), (15, 15), and (0, 20).
The objective function is $Z = px + qy$, where $p > 0$ and $q > 0$.
We are given that the maximum value of Z occurs at both the points (15, 15) and (0, 20).
This implies that the value of the objective function $Z$ is the same at these two points, and this value is the maximum value.
Let's evaluate Z at point (15, 15):
$Z_{(15, 15)} = p(15) + q(15) = 15p + 15q$
Let's evaluate Z at point (0, 20):
$Z_{(0, 20)} = p(0) + q(20) = 0 + 20q = 20q$
Since the maximum occurs at both points, the values of Z must be equal:
$15p + 15q = 20q$
Now, we solve for the relationship between p and q:
$15p = 20q - 15q$
$15p = 5q$
Divide both sides by 5:
$\frac{15p}{5} = \frac{5q}{5}$
$3p = q$
or
$q = 3p$
This is the condition on p and q for the maximum of Z to occur at both (15, 15) and (0, 20).
Comparing this condition with the given options:
(A) $p = q$
(B) $p = 2q$
(C) $q = 2p$
(D) $q = 3p$
The condition $q = 3p$ matches option (D).
The correct option is $\mathbf{(D)}$.
Example 8: Feasible region (shaded) for a LPP is shown in the Fig. 14.6. Minimum of Z = 4x + 3y occurs at the point
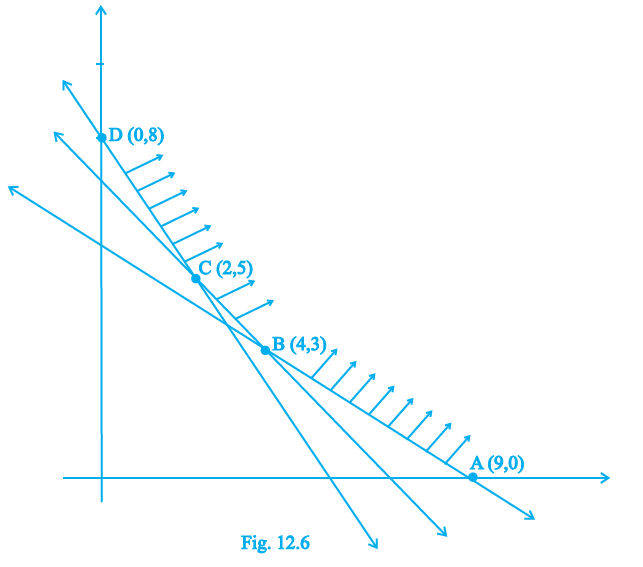
(A) (0, 8)
(B) (2, 5)
(C) (4, 3)
(D) (9, 0)
Answer:
The objective function to be minimised is $Z = 4x + 3y$.
The feasible region is shown in the given figure. The corner points (vertices) of this feasible region are explicitly marked in the figure or can be identified as the intersection points of the boundary lines. The corner points are:
- (0, 8)
- (2, 5)
- (4, 3)
- (9, 0)
The feasible region appears to be the quadrilateral formed by these points in the first quadrant, along with the constraints $x \ge 0$ and $y \ge 0$. Since the region is bounded, the minimum value of Z will occur at one of these corner points.
We evaluate the objective function $Z = 4x + 3y$ at each of these corner points:
At the point (0, 8):
$Z = 4(0) + 3(8) = 0 + 24 = 24$
At the point (2, 5):
$Z = 4(2) + 3(5) = 8 + 15 = 23$
At the point (4, 3):
$Z = 4(4) + 3(3) = 16 + 9 = 25$
At the point (9, 0):
$Z = 4(9) + 3(0) = 36 + 0 = 36$
We can list the values of Z in a table:
| Corner Point (x, y) | Value of $Z = 4x + 3y$ |
| (0, 8) | 24 |
| (2, 5) | 23 |
| (4, 3) | 25 |
| (9, 0) | 36 |
Comparing the values of Z, the minimum value is 23.
The minimum value of Z occurs at the point (2, 5).
Therefore, the correct option is (B).
The correct option is $\mathbf{(B)}$.
Example 9 to 10 (Fill in the Blanks)
Fill in the blanks in each of the Examples 9 and 10:
Example 9: In a LPP, the linear function which has to be maximised or minimised is called a linear __________ function.
Answer:
In a LPP, the linear function which has to be maximised or minimised is called a linear objective function.
The blank should be filled with the word "objective".
Example 10: The common region determined by all the linear constraints of a LPP is called the _______ region.
Answer:
The common region determined by all the linear constraints of a LPP is called the feasible region.
The blank should be filled with the word "feasible".
Example 11 to 12 (True or False)
State whether the statements in Examples 11 and 12 are True or False.
Example 11: If the feasible region for a linear programming problem is bounded, then the objective function Z = ax + by has both a maximum and a minimum value on R.
Answer:
The statement is True.
According to the Fundamental Theorem of Linear Programming, if the feasible region for a linear programming problem is a bounded convex polygon, then the objective function has both a maximum and a minimum value, and these occur at the corner points (vertices) of the feasible region.
Here, R represents the feasible region. If the feasible region is bounded, then the objective function $Z = ax + by$ is guaranteed to have both a maximum and a minimum value within that region.
Example 12: The minimum value of the objective function Z = ax + by in a linear programming problem always occurs at only one corner point of the feasible region.
Answer:
The statement is False.
While the optimal value (maximum or minimum) of the objective function in a Linear Programming Problem always occurs at a corner point of the feasible region (if an optimal solution exists), it is not always true that it occurs at only one corner point.
If the objective function is parallel to one of the boundary lines of the feasible region, and that boundary line contains multiple corner points, then the optimal value can occur at more than one corner point and at every point on the line segment connecting these corner points.
Exercise
Question 1 to 15 (Short Answer Type Questions)
Question 1. Determine the maximum value of Z = 11x + 7y subject to the constraints :
2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
Answer:
Given:
Objective function to maximize: $Z = 11x + 7y$
Constraints:
$2x + y \leq 6$
$x \leq 2$
$x \geq 0$
$y \geq 0$
To Find:
The maximum value of Z subject to the given constraints.
Solution:
The given constraints are linear inequalities. The region satisfying all constraints simultaneously is the feasible region.
The constraints $x \geq 0$ and $y \geq 0$ indicate that the feasible region lies in the first quadrant.
Consider the boundary lines corresponding to the other inequalities:
$2x + y = 6$
$x = 2$
We find the vertices (corner points) of the feasible region formed by the intersection of these boundary lines and the axes ($x=0, y=0$).
1. Intersection of $x=0$ and $y=0$: Point (0, 0).
2. Intersection of $y=0$ and $x=2$: Point (2, 0).
3. Intersection of $x=2$ and $2x + y = 6$. Substitute $x=2$ into the equation $2x + y = 6$:
$2(2) + y = 6$
$4 + y = 6$
$y = 6 - 4$
$y = 2$
Point: (2, 2).
4. Intersection of $x=0$ and $2x + y = 6$. Substitute $x=0$ into the equation $2x + y = 6$:
$2(0) + y = 6$
$0 + y = 6$
$y = 6$
Point: (0, 6).
The vertices of the feasible region are (0, 0), (2, 0), (2, 2), and (0, 6).
Now, we evaluate the objective function $Z = 11x + 7y$ at each vertex:
| Vertex (x, y) | Value of Z = 11x + 7y |
| (0, 0) | $Z = 11(0) + 7(0) = 0$ |
| (2, 0) | $Z = 11(2) + 7(0) = 22 + 0 = 22$ |
| (2, 2) | $Z = 11(2) + 7(2) = 22 + 14 = 36$ |
| (0, 6) | $Z = 11(0) + 7(6) = 0 + 42 = 42$ |
Comparing the values of Z at the vertices, the maximum value is 42.
Conclusion:
The maximum value of Z is 42, which occurs at the point (0, 6).
Question 2. Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0.
Answer:
Given:
Objective function to maximize: $Z = 3x + 4y$
Constraints:
$x + y \leq 1$
$x \geq 0$
$y \geq 0$
To Find:
The maximum value of Z subject to the given constraints.
Solution:
The given constraints define the feasible region. The constraints $x \geq 0$ and $y \geq 0$ indicate that the feasible region is in the first quadrant.
The inequality $x + y \leq 1$ is bounded by the line $x + y = 1$.
To find the feasible region, we consider the boundary line $x + y = 1$ and the axes $x = 0, y = 0$.
The vertices (corner points) of the feasible region are the intersections of these lines:
1. Intersection of $x=0$ and $y=0$: Point (0, 0).
2. Intersection of $y=0$ and $x + y = 1$. Substitute $y=0$ into $x + y = 1$:
$x + 0 = 1$
$x = 1$
Point: (1, 0).
3. Intersection of $x=0$ and $x + y = 1$. Substitute $x=0$ into $x + y = 1$:
$0 + y = 1$
$y = 1$
Point: (0, 1).
The vertices of the feasible region are (0, 0), (1, 0), and (0, 1).
Now, we evaluate the objective function $Z = 3x + 4y$ at each vertex:
| Vertex (x, y) | Value of Z = 3x + 4y |
| (0, 0) | $Z = 3(0) + 4(0) = 0$ |
| (1, 0) | $Z = 3(1) + 4(0) = 3 + 0 = 3$ |
| (0, 1) | $Z = 3(0) + 4(1) = 0 + 4 = 4$ |
Comparing the values of Z at the vertices, the maximum value is 4.
Conclusion:
The maximum value of Z is 4, which occurs at the point (0, 1).
Question 3. Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
Answer:
Given:
Objective function to maximize: $Z = 11x + 7y$
Constraints:
$x \leq 3$
$y \leq 2$
$x \geq 0$
$y \geq 0$
To Find:
The maximum value of Z subject to the given constraints.
Solution:
The given constraints define the feasible region. The constraints $x \geq 0$ and $y \geq 0$ restrict the region to the first quadrant.
The constraint $x \leq 3$ is the region to the left of or on the vertical line $x = 3$.
The constraint $y \leq 2$ is the region below or on the horizontal line $y = 2$.
The feasible region is the rectangle bounded by the lines $x=0$, $y=0$, $x=3$, and $y=2$.
The vertices (corner points) of this feasible region are the intersections of these boundary lines:
1. Intersection of $x=0$ and $y=0$: Point (0, 0).
2. Intersection of $y=0$ and $x=3$: Point (3, 0).
3. Intersection of $x=3$ and $y=2$: Point (3, 2).
4. Intersection of $y=2$ and $x=0$: Point (0, 2).
The vertices of the feasible region are (0, 0), (3, 0), (3, 2), and (0, 2).
Now, we evaluate the objective function $Z = 11x + 7y$ at each vertex:
| Vertex (x, y) | Value of Z = 11x + 7y |
| (0, 0) | $Z = 11(0) + 7(0) = 0 + 0 = 0$ |
| (3, 0) | $Z = 11(3) + 7(0) = 33 + 0 = 33$ |
| (3, 2) | $Z = 11(3) + 7(2) = 33 + 14 = 47$ |
| (0, 2) | $Z = 11(0) + 7(2) = 0 + 14 = 14$ |
Comparing the values of Z at the vertices, the maximum value is 47.
Conclusion:
The maximum value of Z is 47, which occurs at the point (3, 2).
Question 4. Minimise Z = 13x – 15y subject to the constraints : x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0.
Answer:
Given:
Objective function to minimize: $Z = 13x – 15y$
Constraints:
$x + y \leq 7$
$2x – 3y + 6 \geq 0$
$x \geq 0$
$y \geq 0$
To Find:
The minimum value of Z subject to the given constraints.
Solution:
The constraints define the feasible region. The conditions $x \geq 0$ and $y \geq 0$ restrict the feasible region to the first quadrant.
We consider the boundary lines corresponding to the inequalities:
1. $x + y = 7$
2. $2x – 3y + 6 = 0 \implies 2x - 3y = -6$
We identify the vertices (corner points) of the feasible region, which are the intersection points of these boundary lines within the first quadrant.
1. Intersection of $x=0$ and $y=0$: Point (0, 0). This point satisfies $0+0 \leq 7$ and $2(0)-3(0)+6 \geq 0$. So, (0, 0) is a vertex.
2. Intersection of $y=0$ and $x+y=7$: Setting $y=0$ in $x+y=7$, we get $x=7$. Point (7, 0). This point satisfies $2(7)-3(0)+6 = 14+6 = 20 \geq 0$. So, (7, 0) is a vertex.
3. Intersection of $x=0$ and $2x-3y=-6$: Setting $x=0$ in $2x-3y=-6$, we get $-3y=-6 \implies y=2$. Point (0, 2). This point satisfies $0+2 \leq 7$. So, (0, 2) is a vertex.
4. Intersection of $x+y=7$ and $2x-3y=-6$.
From $x+y=7$, we have $y = 7-x$. Substitute this into the second equation:
$2x - 3(7-x) = -6$
$2x - 21 + 3x = -6$
$5x = 21 - 6$
$5x = 15$
$x = 3$
Substitute $x=3$ back into $y=7-x$:
$y = 7 - 3$
$y = 4$
Point: (3, 4). This point is in the first quadrant and satisfies both inequalities as shown in the vertex finding step above. So, (3, 4) is a vertex.
The vertices of the feasible region are (0, 0), (7, 0), (0, 2), and (3, 4).
Now, we evaluate the objective function $Z = 13x - 15y$ at each vertex:
| Vertex (x, y) | Value of Z = 13x – 15y |
| (0, 0) | $Z = 13(0) - 15(0) = 0 - 0 = 0$ |
| (7, 0) | $Z = 13(7) - 15(0) = 91 - 0 = 91$ |
| (0, 2) | $Z = 13(0) - 15(2) = 0 - 30 = -30$ |
| (3, 4) | $Z = 13(3) - 15(4) = 39 - 60 = -21$ |
Comparing the values of Z at the vertices, the minimum value is -30.
Conclusion:
The minimum value of Z is -30, which occurs at the point (0, 2).
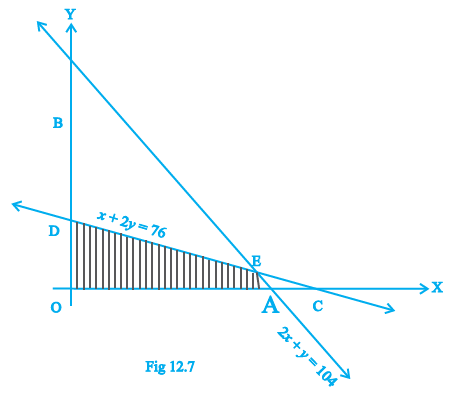
Question 5. Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Fig.12.7.
Answer:
Given:
Objective function to maximize: $Z = 3x + 4y$
The feasible region is shown in Fig. 12.7.
To Find:
The maximum value of Z over the given feasible region.
Solution:
From the provided figure (Fig. 12.7), the vertices (corner points) of the feasible region are clearly visible. These vertices are where the boundary lines of the inequalities intersect.
The vertices of the feasible region are:
(0, 0)
(1, 0)
(0, 1)
To find the maximum value of the objective function $Z = 3x + 4y$, we evaluate Z at each of these vertices.
| Vertex (x, y) | Value of Z = 3x + 4y |
| (0, 0) | $Z = 3(0) + 4(0) = 0 + 0 = 0$ |
| (1, 0) | $Z = 3(1) + 4(0) = 3 + 0 = 3$ |
| (0, 1) | $Z = 3(0) + 4(1) = 0 + 4 = 4$ |
By comparing the values of Z at these vertices, we find the maximum value.
The values obtained are 0, 3, and 4.
The maximum value among these is 4.
Conclusion:
The maximum value of Z is 4, which occurs at the vertex (0, 1).
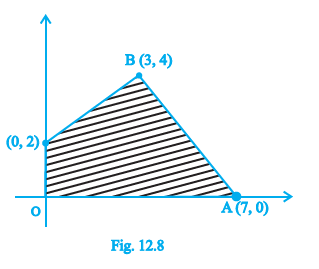
Question 6. Feasible region (shaded) for a LPP is shown in Fig. 12.8.
Maximise Z = 5x + 7y.
Answer:
Given:
Objective function to maximize: $Z = 5x + 7y$
The feasible region is shown in Fig. 12.8.
To Find:
The maximum value of Z over the given feasible region.
Solution:
The vertices (corner points) of the feasible region are the points where the boundary lines intersect. From the provided figure (Fig. 12.8), the vertices of the shaded feasible region are clearly identified.
The vertices are:
(0, 0)
(5, 0)
(3, 4)
(0, 5)
According to the fundamental theorem of linear programming, the optimal solution (maximum or minimum) of the objective function, if it exists, occurs at one of the vertices of the feasible region.
We evaluate the objective function $Z = 5x + 7y$ at each of these vertices:
| Vertex (x, y) | Value of Z = 5x + 7y |
| (0, 0) | $Z = 5(0) + 7(0) = 0 + 0 = 0$ |
| (5, 0) | $Z = 5(5) + 7(0) = 25 + 0 = 25$ |
| (3, 4) | $Z = 5(3) + 7(4) = 15 + 28 = 43$ |
| (0, 5) | $Z = 5(0) + 7(5) = 0 + 35 = 35$ |
Comparing the values of Z calculated at the vertices, we can determine the maximum value.
The values are 0, 25, 43, and 35.
The maximum value among these is 43.
Conclusion:
The maximum value of Z is 43, which occurs at the vertex (3, 4).
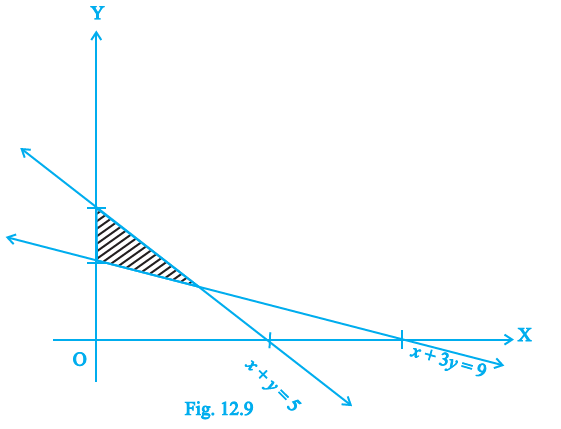
Question 7. The feasible region for a LPP is shown in Fig. 12.9. Find the minimum value of Z = 11x + 7y.
Answer:
Given:
Objective function to minimize: $Z = 11x + 7y$
The feasible region is shown in Fig. 12.9.
To Find:
The minimum value of Z over the given feasible region.
Solution:
The vertices (corner points) of the feasible region shown in Fig. 12.9 are the points where the boundary lines intersect. These vertices are:
From the figure, we can identify the vertices:
(0, 0)
(6, 0)
(0, 9)
The intersection point of the two lines forming the boundary of the feasible region is also a vertex. By observing the graph, this intersection point appears to be (2, 4).
Let's confirm the equations of the lines from the points they pass through:
Line 1 passes through (6, 0) and (2, 4). The equation is $\frac{y - 0}{x - 6} = \frac{4 - 0}{2 - 6} = \frac{4}{-4} = -1$.
$y = -1(x - 6)$
$y = -x + 6 \implies x + y = 6$.
Line 2 passes through (0, 9) and (2, 4). The equation is $\frac{y - 9}{x - 0} = \frac{4 - 9}{2 - 0} = \frac{-5}{2}$.
$2(y - 9) = -5x$
$2y - 18 = -5x \implies 5x + 2y = 18$.
The intersection of $x + y = 6$ and $5x + 2y = 18$ can be found by solving the system of equations.
From $x+y=6$, $y = 6-x$. Substituting into the second equation:
$5x + 2(6-x) = 18$
$5x + 12 - 2x = 18$
$3x = 18 - 12$
$3x = 6$
$x = 2$
Substituting $x=2$ into $y=6-x$:
$y = 6 - 2 = 4$.
So the intersection point is indeed (2, 4).
The vertices of the feasible region are (0, 0), (6, 0), (2, 4), and (0, 9).
Now, we evaluate the objective function $Z = 11x + 7y$ at each vertex:
| Vertex (x, y) | Value of Z = 11x + 7y |
| (0, 0) | $Z = 11(0) + 7(0) = 0 + 0 = 0$ |
| (6, 0) | $Z = 11(6) + 7(0) = 66 + 0 = 66$ |
| (2, 4) | $Z = 11(2) + 7(4) = 22 + 28 = 50$ |
| (0, 9) | $Z = 11(0) + 7(9) = 0 + 63 = 63$ |
Comparing the values of Z at the vertices, we find the minimum value.
The values are 0, 66, 50, and 63.
The minimum value among these is 0.
Conclusion:
The minimum value of Z is 0, which occurs at the vertex (0, 0).
Question 8. Refer to Exercise 7 above. Find the maximum value of Z.
Answer:
Given:
Objective function to maximize: $Z = 11x + 7y$
The feasible region is the same as in Exercise 7, shown in Fig. 12.9.
To Find:
The maximum value of Z over the feasible region from Fig. 12.9.
Solution:
As determined in the solution to Exercise 7, the vertices (corner points) of the feasible region shown in Fig. 12.9 are:
(0, 0)
(6, 0)
(2, 4)
(0, 9)
To find the maximum value of the objective function $Z = 11x + 7y$, we evaluate Z at each of these vertices:
| Vertex (x, y) | Value of Z = 11x + 7y |
| (0, 0) | $Z = 11(0) + 7(0) = 0 + 0 = 0$ |
| (6, 0) | $Z = 11(6) + 7(0) = 66 + 0 = 66$ |
| (2, 4) | $Z = 11(2) + 7(4) = 22 + 28 = 50$ |
| (0, 9) | $Z = 11(0) + 7(9) = 0 + 63 = 63$ |
Comparing the values of Z calculated at the vertices, we identify the maximum value.
The values are 0, 66, 50, and 63.
The maximum value among these is 66.
Conclusion:
The maximum value of Z is 66, which occurs at the vertex (6, 0).
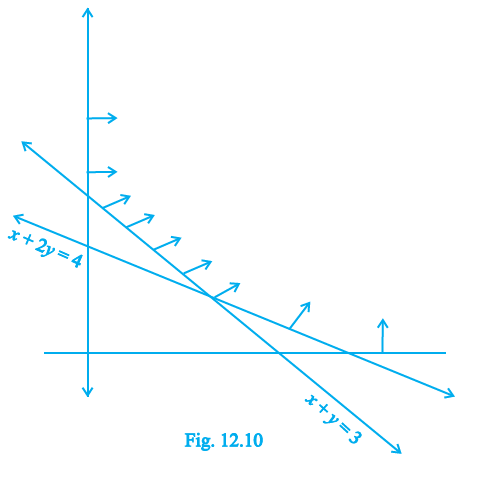
Question 9. The feasible region for a LPP is shown in Fig. 12.10. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists.
Answer:
Given:
Objective function to minimize: $Z = 4x + y$
The feasible region is shown in Fig. 12.10.
To Find:
The minimum value of Z over the given feasible region, if it exists.
Solution:
From the provided figure (Fig. 12.10), we can identify the corner points (vertices) of the feasible region. These are the points where the boundary lines intersect.
The vertices of the feasible region are:
(0, 3)
(1, 2)
(6, 0)
We evaluate the objective function $Z = 4x + y$ at each of these vertices:
| Vertex (x, y) | Value of Z = 4x + y |
| (0, 3) | $Z = 4(0) + 3 = 0 + 3 = 3$ |
| (1, 2) | $Z = 4(1) + 2 = 4 + 2 = 6$ |
| (6, 0) | $Z = 4(6) + 0 = 24 + 0 = 24$ |
The values of Z at the corner points are 3, 6, and 24.
The smallest value among these is 3.
Since the feasible region is unbounded, we need to check if the minimum value actually exists.
The feasible region is defined by constraints which are '$\geq$' type inequalities ($x+y \geq 3$, $2x+5y \geq 12$, $x \geq 0$, $y \geq 0$). The coefficients of x and y in the objective function $Z = 4x + y$ (which are 4 and 1) are both positive. In such cases, for an unbounded feasible region, the minimum value of the objective function always exists and occurs at a corner point.
Alternatively, consider the inequality $4x + y < 3$. This represents the region below the line $4x + y = 3$. The line $4x + y = 3$ passes through the vertex (0, 3).
We check if there is any point in the feasible region (other than (0, 3)) that also lies in the region $4x + y < 3$.
The feasible region lies above or on the boundary lines $x+y=3$ and $2x+5y=12$. The slope of the line $4x+y=3$ (slope -4) is steeper than the slopes of the boundary lines ($x+y=3$ has slope -1, $2x+5y=12$ has slope -0.4).
As we move away from the origin within the feasible region, the value of $4x+y$ increases because the coefficients 4 and 1 are positive.
Since the feasible region is above or on the line $4x+y=3$ (at point (0,3)), there are no points in the feasible region for which $4x+y < 3$.
Therefore, the minimum value of Z exists and is the smallest value found at the vertices.
Conclusion:
The minimum value of Z is 3, which occurs at the vertex (0, 3).
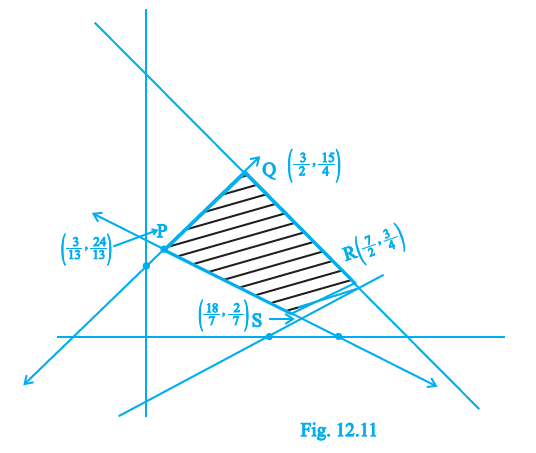
Question 10. In Fig. 12.11, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y
Answer:
Given:
Objective function: $Z = x + 2y$
The feasible region is the shaded area shown in Fig. 12.11.
To Find:
The maximum and minimum values of Z over the given feasible region.
Solution:
The feasible region in the figure is a polygon. The vertices (corner points) of this feasible region are clearly marked in the figure. These vertices are:
(0, 0)
(10, 0)
(6, 4)
(4, 5)
(0, 5)
According to the fundamental theorem of linear programming, for a closed and bounded feasible region, the maximum and minimum values of the objective function occur at the vertices of the feasible region.
We evaluate the objective function $Z = x + 2y$ at each of these vertices:
| Vertex (x, y) | Value of Z = x + 2y |
| (0, 0) | $Z = 0 + 2(0) = 0$ |
| (10, 0) | $Z = 10 + 2(0) = 10 + 0 = 10$ |
| (6, 4) | $Z = 6 + 2(4) = 6 + 8 = 14$ |
| (4, 5) | $Z = 4 + 2(5) = 4 + 10 = 14$ |
| (0, 5) | $Z = 0 + 2(5) = 0 + 10 = 10$ |
Comparing the values of Z calculated at the vertices, we find the minimum and maximum values.
The values are 0, 10, 14, 14, and 10.
The minimum value among these is 0.
The maximum value among these is 14.
Conclusion:
The minimum value of Z is 0, which occurs at the vertex (0, 0).
The maximum value of Z is 14, which occurs at the vertices (6, 4) and (4, 5).
Question 11. A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B.
Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60, formulate this problem as a LPP so that the manufacturer can maximise his profit.
Answer:
Given:
Stock of components:
Resistors: 200
Transistors: 120
Capacitors: 150
Requirements per circuit:
Type A: 20 resistors, 10 transistors, 10 capacitors
Type B: 10 resistors, 20 transistors, 30 capacitors
Profit per circuit:
Type A: $\textsf{₹}50$
Type B: $\textsf{₹}60$
To Formulate:
Formulate the problem as a Linear Programming Problem (LPP) to maximize the manufacturer's profit.
Formulation:
Let $x$ be the number of Type A circuits produced.
Let $y$ be the number of Type B circuits produced.
These are our decision variables.
The manufacturer wants to maximize the total profit. The profit from Type A circuits is $50x$, and the profit from Type B circuits is $60y$.
The objective function to maximize is:
$Z = 50x + 60y$
The production is subject to the availability of components. We have constraints based on the total number of resistors, transistors, and capacitors used.
Constraints:
1. Constraint on Resistors:
Total resistors used = (Resistors for Type A) + (Resistors for Type B)
Total resistors used = $20x + 10y$
Since the total resistors available are 200:
$20x + 10y \leq 200$
Dividing by 10, we get:
$2x + y \leq 20$
2. Constraint on Transistors:
Total transistors used = (Transistors for Type A) + (Transistors for Type B)
Total transistors used = $10x + 20y$
Since the total transistors available are 120:
$10x + 20y \leq 120$
Dividing by 10, we get:
$x + 2y \leq 12$
3. Constraint on Capacitors:
Total capacitors used = (Capacitors for Type A) + (Capacitors for Type B)
Total capacitors used = $10x + 30y$
Since the total capacitors available are 150:
$10x + 30y \leq 150$
Dividing by 10, we get:
$x + 3y \leq 15$
Additionally, the number of circuits produced cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
The Linear Programming Problem is:
Maximize $Z = 50x + 60y$
Subject to the constraints:
$2x + y \leq 20$
$x + 2y \leq 12$
$x + 3y \leq 15$
$x \geq 0$
$y \geq 0$
Question 12. A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent on the job and the number of large vans can not exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
Answer:
Given:
Total packages to transport: 1200
Large vans:
Capacity: 200 packages
Cost: $\textsf{₹}400$ per van
Small vans:
Capacity: 80 packages
Cost: $\textsf{₹}200$ per van
Total budget for the job: Not more than $\textsf{₹}3000$
Constraint on number of vans: Number of large vans cannot exceed the number of small vans.
Objective: Minimise the total cost.
To Formulate:
Formulate the problem as a Linear Programming Problem (LPP) to minimize the transportation cost.
Formulation:
Let $x$ be the number of large vans used.
Let $y$ be the number of small vans used.
These are our decision variables.
The firm wants to minimize the total cost of engaging vans. The cost for large vans is $400x$, and the cost for small vans is $200y$.
The objective function to minimize is:
$Z = 400x + 200y$
The transportation must satisfy the given conditions, which form the constraints.
Constraints:
1. Constraint on total packages transported:
Total packages carried = (Packages by large vans) + (Packages by small vans)
Total packages carried = $200x + 80y$
The firm must transport at least 1200 packages:
$200x + 80y \geq 1200$
Dividing by 40, we get:
$5x + 2y \geq 30$
2. Constraint on total cost:
Total cost = (Cost of large vans) + (Cost of small vans)
Total cost = $400x + 200y$
The total cost must not exceed $\textsf{₹}3000$:
$400x + 200y \leq 3000$
Dividing by 100, we get:
$4x + 2y \leq 30$
Dividing by 2, we get:
$2x + y \leq 15$
3. Constraint on the number of large and small vans:
The number of large vans cannot exceed the number of small vans:
$x \leq y$
This can be written as:
$x - y \leq 0$
Also, the number of vans must be non-negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
Since the number of vans must be whole numbers, $x$ and $y$ are also restricted to be integers (although this is not explicitly required in standard LPP formulation unless specified as Integer Programming). For a general LPP formulation, non-negativity is sufficient.
The Linear Programming Problem is:
Minimize $Z = 400x + 200y$
Subject to the constraints:
$5x + 2y \geq 30$
$2x + y \leq 15$
$x - y \leq 0$
$x \geq 0$
$y \geq 0$
Question 13. A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours.
On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws.
Formulate this problem as a LPP given that the objective is to maximise profit.
Answer:
Given:
Machine availability per week: 60 hours for each machine.
1 hour = 60 minutes, so 60 hours = $60 \times 60 = 3600$ minutes.
Machine requirements per box:
Type A: 2 min (threading), 3 min (slotting)
Type B: 8 min (threading), 2 min (slotting)
Profit per box:
Type A: $\textsf{₹}100$
Type B: $\textsf{₹}170$
To Formulate:
Formulate the problem as a Linear Programming Problem (LPP) to maximize the total profit.
Formulation:
Let $x$ be the number of boxes of Type A screws manufactured per week.
Let $y$ be the number of boxes of Type B screws manufactured per week.
These are the decision variables.
The objective is to maximize the total profit. The profit is given by the number of boxes of each type multiplied by their respective profits per box.
The objective function to maximize is:
$Z = 100x + 170y$
The constraints are based on the available time for each machine.
Constraints:
1. Constraint on Threading Machine time:
Total threading time used = (Time for $x$ boxes of A) + (Time for $y$ boxes of B)
Total threading time used = $2x + 8y$ minutes
Available threading time = 3600 minutes
The total time used cannot exceed the available time:
$2x + 8y \leq 3600$
This inequality can be simplified by dividing by 2:
$x + 4y \leq 1800$
2. Constraint on Slotting Machine time:
Total slotting time used = (Time for $x$ boxes of A) + (Time for $y$ boxes of B)
Total slotting time used = $3x + 2y$ minutes
Available slotting time = 3600 minutes
The total time used cannot exceed the available time:
$3x + 2y \leq 3600$
Finally, the number of boxes manufactured cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
The Linear Programming Problem is:
Maximize $Z = 100x + 170y$
Subject to the constraints:
$x + 4y \leq 1800$
$3x + 2y \leq 3600$
$x \geq 0$
$y \geq 0$
Question 14. A company manufactures two types of sweaters : type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater. The company can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B.
Formulate this problem as a LPP to maximise the profit to the company.
Answer:
Given:
Cost of making sweaters:
Type A: $\textsf{₹}360$ per sweater
Type B: $\textsf{₹}120$ per sweater
Maximum total sweaters per day: 300
Maximum total cost per day: $\textsf{₹}72000$
Constraint on numbers: Number of type B sweaters cannot exceed number of type A sweaters by more than 100.
Profit per sweater:
Type A: $\textsf{₹}200$
Type B: $\textsf{₹}120$
Objective: Maximise the total profit.
To Formulate:
Formulate the problem as a Linear Programming Problem (LPP) to maximize the company's profit.
Formulation:
Let $x$ be the number of type A sweaters manufactured per day.
Let $y$ be the number of type B sweaters manufactured per day.
These are our decision variables.
The objective is to maximize the total profit. The profit from type A sweaters is $200x$, and the profit from type B sweaters is $120y$.
The objective function to maximize is:
$Z = 200x + 120y$
The production is subject to several constraints.
Constraints:
1. Constraint on total number of sweaters:
The total number of sweaters cannot exceed 300:
$x + y \leq 300$
2. Constraint on total cost:
Total cost = (Cost of A sweaters) + (Cost of B sweaters)
Total cost = $360x + 120y$
The total cost must not exceed $\textsf{₹}72000$:
$360x + 120y \leq 72000$
This inequality can be simplified by dividing by 120:
$\frac{360x}{120} + \frac{120y}{120} \leq \frac{72000}{120}$
$3x + y \leq 600$
3. Constraint on the relative number of sweaters:
The number of type B sweaters ($y$) cannot exceed the number of type A sweaters ($x$) by more than 100.
$y \leq x + 100$
This can be rewritten as:
$y - x \leq 100$
Or:
$-x + y \leq 100$
Also, the number of sweaters manufactured cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
The Linear Programming Problem is:
Maximize $Z = 200x + 120y$
Subject to the constraints:
$x + y \leq 300$
$3x + y \leq 600$
$-x + y \leq 100$
$x \geq 0$
$y \geq 0$
Question 15. A man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel.
Express this problem as a linear programming problem.
Answer:
Given:
Speed 1 ($v_1$): 50 km/hour, Cost 1 ($c_1$): $\textsf{₹}2$/km
Speed 2 ($v_2$): 80 km/hour, Cost 2 ($c_2$): $\textsf{₹}3$/km
Maximum petrol cost: $\textsf{₹}120$
Maximum time: 1 hour
Objective: Maximize total distance travelled.
To Formulate:
Formulate the problem as a Linear Programming Problem (LPP) to maximize the distance travelled.
Formulation:
Let $x$ be the distance (in km) travelled at the speed of 50 km/hour.
Let $y$ be the distance (in km) travelled at the speed of 80 km/hour.
These are our decision variables.
The objective is to maximize the total distance travelled, which is the sum of the distances travelled at each speed.
The objective function to maximize is:
$Z = x + y$
The constraints are based on the total cost of petrol and the total time taken for the journey.
Constraints:
1. Constraint on total petrol cost:
Cost for distance $x$ at $\textsf{₹}2$/km is $2x$.
Cost for distance $y$ at $\textsf{₹}3$/km is $3y$.
Total cost = $2x + 3y$.
The total cost must be at most $\textsf{₹}120$:
$2x + 3y \leq 120$
2. Constraint on total time taken:
Time = $\frac{\text{Distance}}{\text{Speed}}$.
Time taken for distance $x$ at 50 km/hour is $\frac{x}{50}$ hours.
Time taken for distance $y$ at 80 km/hour is $\frac{y}{80}$ hours.
Total time = $\frac{x}{50} + \frac{y}{80}$.
The total time must be at most 1 hour:
$\frac{x}{50} + \frac{y}{80} \leq 1$
To clear the fractions, multiply the inequality by the least common multiple of 50 and 80, which is 400:
$400 \left(\frac{x}{50}\right) + 400 \left(\frac{y}{80}\right) \leq 400(1)$
$8x + 5y \leq 400$
Also, the distances travelled cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
The Linear Programming Problem is:
Maximize $Z = x + y$
Subject to the constraints:
$2x + 3y \leq 120$
$8x + 5y \leq 400$
$x \geq 0$
$y \geq 0$
Question 16 to 25 (Long Answer Type Questions)
Question 16. Refer to Exercise 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximise his profit? Determine the maximum profit.
Answer:
Given:
The Linear Programming Problem formulated in Exercise 11 is:
Maximize $Z = 50x + 60y$
Subject to the constraints:
$2x + y \leq 20$
$x + 2y \leq 12$
$x + 3y \leq 15$
$x \geq 0, y \geq 0$
where $x$ is the number of Type A circuits and $y$ is the number of Type B circuits.
To Find:
The number of Type A and Type B circuits to produce to maximize profit, and the maximum profit.
Solution:
To solve this LPP using the graphical method, we first determine the feasible region defined by the given constraints. The constraints $x \geq 0$ and $y \geq 0$ restrict the feasible region to the first quadrant.
We consider the boundary lines of the other inequalities:
1. $2x + y = 20$
2. $x + 2y = 12$
3. $x + 3y = 15$
We find the vertices (corner points) of the feasible region formed by the intersection of these boundary lines and the axes within the first quadrant.
The vertices of the feasible region are:
A: Intersection of $x=0$ and $y=0$ $\implies$ (0, 0).
B: Intersection of $y=0$ and $2x + y = 20$. Setting $y=0$, $2x=20 \implies x=10$. Point (10, 0). This point satisfies $10+2(0)=10 \leq 12$ and $10+3(0)=10 \leq 15$. Feasible.
C: Intersection of $x=0$ and $x + 3y = 15$. Setting $x=0$, $3y=15 \implies y=5$. Point (0, 5). This point satisfies $2(0)+5=5 \leq 20$ and $0+2(5)=10 \leq 12$. Feasible.
D: Intersection of $x + 2y = 12$ and $x + 3y = 15$. Subtracting the first from the second gives $y=3$. Substituting $y=3$ into $x+2y=12$ gives $x+6=12 \implies x=6$. Point (6, 3). This point satisfies $2(6)+3=15 \leq 20$. Feasible.
E: Intersection of $2x + y = 20$ and $x + 2y = 12$. Multiply the second equation by 2: $2x + 4y = 24$. Subtract the first equation ($2x+y=20$) from this: $(2x+4y) - (2x+y) = 24-20 \implies 3y=4 \implies y=4/3$. Substitute $y=4/3$ into $2x+y=20$: $2x + 4/3 = 20 \implies 2x = 20 - 4/3 = 56/3 \implies x = 28/3$. Point (28/3, 4/3). This point satisfies $28/3 + 3(4/3) = 28/3 + 4 = (28+12)/3 = 40/3 = 13.33... \leq 15$. Feasible.
The vertices of the feasible region are (0, 0), (10, 0), (28/3, 4/3), (6, 3), and (0, 5).
We now evaluate the objective function $Z = 50x + 60y$ at each vertex:
| Vertex (x, y) | Value of Z = 50x + 60y |
| (0, 0) | $Z = 50(0) + 60(0) = 0$ |
| (10, 0) | $Z = 50(10) + 60(0) = 500 + 0 = 500$ |
| ($\frac{28}{3}$, $\frac{4}{3}$) | $Z = 50(\frac{28}{3}) + 60(\frac{4}{3}) = \frac{1400}{3} + \frac{240}{3} = \frac{1640}{3}$ |
| (6, 3) | $Z = 50(6) + 60(3) = 300 + 180 = 480$ |
| (0, 5) | $Z = 50(0) + 60(5) = 0 + 300 = 300$ |
Comparing the values of Z at the vertices (0, 500, 1640/3, 480, 300), the maximum value is 1640/3.
The maximum profit occurs at the vertex ($\frac{28}{3}, \frac{4}{3}$).
Conclusion:
To maximize profit, the manufacturer should produce $\frac{28}{3}$ circuits of Type A and $\frac{4}{3}$ circuits of Type B.
The maximum profit is $\textsf{₹}\frac{1640}{3}$.
Question 17. Refer to Exercise 12. What will be the minimum cost?
Answer:
Given:
The Linear Programming Problem (LPP) formulated in Exercise 12 is:
Minimize $Z = 400x + 200y$
Subject to the constraints:
$5x + 2y \geq 30$
$2x + y \leq 15$
$x - y \leq 0 \implies x \leq y$
$x \geq 0, y \geq 0$
where $x$ is the number of large vans and $y$ is the number of small vans.
To Find:
The minimum value of the cost function Z.
Solution:
To find the minimum value of Z, we first determine the feasible region defined by the constraints. The constraints $x \geq 0$ and $y \geq 0$ mean the feasible region lies in the first quadrant.
We consider the boundary lines of the inequalities:
1. $5x + 2y = 30$
2. $2x + y = 15$
3. $x = y$
We find the vertices (corner points) of the feasible region by identifying the intersection points of these boundary lines that satisfy all the given constraints.
Let's find the intersections of the boundary lines in the first quadrant:
a) Intersection of $x=0$ and $2x+y=15$: $2(0)+y=15 \implies y=15$. Point (0, 15). Check constraints: $5(0)+2(15)=30 \geq 30$ (True), $0 \leq 15$ (True). This point is feasible.
b) Intersection of $x=0$ and $5x+2y=30$: $5(0)+2y=30 \implies 2y=30 \implies y=15$. Point (0, 15). Same as above.
c) Intersection of $y=x$ and $2x+y=15$: Substitute $y=x$ into $2x+y=15 \implies 2x+x=15 \implies 3x=15 \implies x=5$. Since $y=x$, $y=5$. Point (5, 5). Check constraints: $5(5)+2(5)=25+10=35 \geq 30$ (True). This point is feasible.
d) Intersection of $y=x$ and $5x+2y=30$: Substitute $y=x$ into $5x+2y=30 \implies 5x+2x=30 \implies 7x=30 \implies x=\frac{30}{7}$. Since $y=x$, $y=\frac{30}{7}$. Point ($\frac{30}{7}$, $\frac{30}{7}$). Check constraints: $2(\frac{30}{7})+\frac{30}{7}=\frac{60}{7}+\frac{30}{7}=\frac{90}{7} \approx 12.86 \leq 15$ (True). This point is feasible.
e) Intersection of $2x+y=15$ and $5x+2y=30$: Multiply the first equation by 2: $4x+2y=30$. Subtract this from the second equation: $(5x+2y)-(4x+2y) = 30-30 \implies x=0$. Substitute $x=0$ into $2x+y=15 \implies 2(0)+y=15 \implies y=15$. Point (0, 15). Same as a) and b).
The vertices of the feasible region are the points (0, 15), (5, 5), and ($\frac{30}{7}$, $\frac{30}{7}$).
We evaluate the objective function $Z = 400x + 200y$ at each of these vertices:
| Vertex (x, y) | Value of Z = 400x + 200y |
| (0, 15) | $Z = 400(0) + 200(15) = 0 + 3000 = 3000$ |
| (5, 5) | $Z = 400(5) + 200(5) = 2000 + 1000 = 3000$ |
| ($\frac{30}{7}$, $\frac{30}{7}$) | $Z = 400(\frac{30}{7}) + 200(\frac{30}{7}) = \frac{12000}{7} + \frac{6000}{7} = \frac{18000}{7}$ |
Comparing the values of Z at the vertices: $3000$, $3000$, and $\frac{18000}{7}$.
We calculate $\frac{18000}{7} \approx 2571.43$.
The minimum value is the smallest among 3000, 3000, and $\frac{18000}{7}$.
The minimum value is $\frac{18000}{7}$.
Conclusion:
The minimum cost is $\textsf{₹}\frac{18000}{7}$, which occurs when using $\frac{30}{7}$ large vans and $\frac{30}{7}$ small vans.
Question 18. Refer to Exercise 13. Solve the linear programming problem and determine the maximum profit to the manufacturer.
Answer:
Given:
The Linear Programming Problem (LPP) formulated in Exercise 13 is:
Maximize $Z = 100x + 170y$
Subject to the constraints:
$x + 4y \leq 1800$
$3x + 2y \leq 3600$
$x \geq 0$
$y \geq 0$
where $x$ is the number of boxes of Type A screws and $y$ is the number of boxes of Type B screws.
To Find:
The number of boxes of Type A and Type B screws to produce to maximize profit, and the maximum profit.
Solution:
To find the maximum profit, we need to find the optimal solution to the LPP by determining the feasible region and evaluating the objective function at its vertices.
The constraints $x \geq 0$ and $y \geq 0$ mean the feasible region lies in the first quadrant.
We consider the boundary lines:
1. $x + 4y = 1800$
2. $3x + 2y = 3600$
We find the vertices (corner points) of the feasible region:
a) Intersection of $x=0$ and $y=0$: Point (0, 0).
b) Intersection of $y=0$ and $3x + 2y = 3600$: Setting $y=0$, $3x = 3600 \implies x = 1200$. Point (1200, 0). Check constraint 1: $1200 + 4(0) = 1200 \leq 1800$. Feasible.
c) Intersection of $x=0$ and $x + 4y = 1800$: Setting $x=0$, $4y = 1800 \implies y = 450$. Point (0, 450). Check constraint 2: $3(0) + 2(450) = 900 \leq 3600$. Feasible.
d) Intersection of $x + 4y = 1800$ and $3x + 2y = 3600$.
Multiply the first equation by 3:
$3(x + 4y) = 3(1800)$
$3x + 12y = 5400$ ... (i)
The second equation is:
$3x + 2y = 3600$ ... (ii)
Subtract equation (ii) from equation (i):
$(3x + 12y) - (3x + 2y) = 5400 - 3600$
$10y = 1800$
$y = 180$
Substitute $y = 180$ into $x + 4y = 1800$:
$x + 4(180) = 1800$
$x + 720 = 1800$
$x = 1800 - 720$
$x = 1080$
Point: (1080, 180).
The vertices of the feasible region are (0, 0), (1200, 0), (1080, 180), and (0, 450).
We evaluate the objective function $Z = 100x + 170y$ at each vertex:
| Vertex (x, y) | Value of Z = 100x + 170y |
| (0, 0) | $Z = 100(0) + 170(0) = 0$ |
| (1200, 0) | $Z = 100(1200) + 170(0) = 120000$ |
| (1080, 180) | $Z = 100(1080) + 170(180) = 108000 + 30600 = 138600$ |
| (0, 450) | $Z = 100(0) + 170(450) = 0 + 76500 = 76500$ |
Comparing the values of Z at the vertices, the maximum value is 138600.
This maximum profit occurs at the point (1080, 180).
Conclusion:
To maximize his profit, the manufacturer should produce 1080 boxes of Type A circuits and 180 boxes of Type B circuits.
The maximum profit will be $\textsf{₹}138600$.
Question 19. Refer to Exercise 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
Answer:
Given:
The Linear Programming Problem (LPP) formulated in Exercise 14 is:
Maximize $Z = 200x + 120y$
Subject to the constraints:
$x + y \leq 300$
$3x + y \leq 600$
$-x + y \leq 100$
$x \geq 0$
$y \geq 0$
where $x$ is the number of type A sweaters and $y$ is the number of type B sweaters manufactured per day.
To Find:
The number of sweaters of each type ($x$ and $y$) that maximize the profit, and the maximum profit value (Z).
Solution:
To solve this LPP, we determine the feasible region defined by the constraints. The constraints $x \geq 0$ and $y \geq 0$ mean the feasible region is in the first quadrant.
We consider the boundary lines of the inequalities:
1. $x + y = 300$
2. $3x + y = 600$
3. $-x + y = 100$
We identify the vertices (corner points) of the feasible region by finding the intersection points of these boundary lines within the first quadrant and satisfying all inequalities.
The vertices of the feasible region are:
a) Intersection of $x=0$ and $y=0$: Point (0, 0).
b) Intersection of $y=0$ and $3x+y=600$: $3x=600 \implies x=200$. Point (200, 0). Check constraints: $200+0 \leq 300$ (True), $-200+0 \leq 100$ (True). Feasible.
c) Intersection of $x=0$ and $-x+y=100$: $y=100$. Point (0, 100). Check constraints: $0+100 \leq 300$ (True), $3(0)+100 \leq 600$ (True). Feasible.
d) Intersection of $x+y=300$ and $3x+y=600$. Subtracting the first equation from the second gives: $(3x+y) - (x+y) = 600 - 300 \implies 2x = 300 \implies x=150$. Substituting $x=150$ into $x+y=300$: $150+y=300 \implies y=150$. Point (150, 150). Check constraint 3: $-150+150=0 \leq 100$ (True). Feasible.
e) Intersection of $x+y=300$ and $-x+y=100$. Adding the two equations gives: $(x+y) + (-x+y) = 300 + 100 \implies 2y = 400 \implies y=200$. Substituting $y=200$ into $x+y=300$: $x+200=300 \implies x=100$. Point (100, 200). Check constraint 2: $3(100)+200 = 300+200 = 500 \leq 600$ (True). Feasible.
The vertices of the feasible region are (0, 0), (200, 0), (0, 100), (150, 150), and (100, 200).
We evaluate the objective function $Z = 200x + 120y$ at each vertex:
| Vertex (x, y) | Value of Z = 200x + 120y |
| (0, 0) | $Z = 200(0) + 120(0) = 0$ |
| (200, 0) | $Z = 200(200) + 120(0) = 40000$ |
| (0, 100) | $Z = 200(0) + 120(100) = 12000$ |
| (150, 150) | $Z = 200(150) + 120(150) = 30000 + 18000 = 48000$ |
| (100, 200) | $Z = 200(100) + 120(200) = 20000 + 24000 = 44000$ |
Comparing the values of Z at the vertices (0, 40000, 12000, 48000, 44000), the maximum value is 48000.
This maximum profit occurs at the vertex (150, 150).
Conclusion:
To maximize the profit, the company should make 150 sweaters of type A and 150 sweaters of type B per day.
The maximum profit will be $\textsf{₹}48000$.
Question 20. Refer to Exercise 15. Determine the maximum distance that the man can travel.
Answer:
Given:
The Linear Programming Problem (LPP) formulated in Exercise 15 is:
Maximize $Z = x + y$
Subject to the constraints:
$2x + 3y \leq 120$
$8x + 5y \leq 400$
$x \geq 0$
$y \geq 0$
where $x$ is the distance travelled at 50 km/h and $y$ is the distance travelled at 80 km/h. The objective function $Z$ represents the total distance travelled.
To Find:
The maximum distance that the man can travel, which is the maximum value of Z.
Solution:
To find the maximum value of the objective function, we use the graphical method. We determine the feasible region defined by the given constraints. The non-negativity constraints $x \geq 0$ and $y \geq 0$ indicate that the feasible region lies in the first quadrant.
We consider the boundary lines for the other constraints:
1. $2x + 3y = 120$
2. $8x + 5y = 400$
We find the vertices (corner points) of the feasible region formed by the intersection of these boundary lines and the axes within the first quadrant.
a) Intersection of $x=0$ and $y=0$: Point (0, 0).
b) Intersection of $y=0$ and $8x + 5y = 400$: Setting $y=0$, $8x = 400 \implies x = 50$. Point (50, 0). Check constraint 1: $2(50) + 3(0) = 100 \leq 120$ (True). Feasible.
c) Intersection of $x=0$ and $2x + 3y = 120$: Setting $x=0$, $3y = 120 \implies y = 40$. Point (0, 40). Check constraint 2: $8(0) + 5(40) = 200 \leq 400$ (True). Feasible.
d) Intersection of $2x + 3y = 120$ and $8x + 5y = 400$.
We can solve this system of equations. Multiply the first equation by 4:
$4(2x + 3y) = 4(120)$
$8x + 12y = 480$
Now subtract the second equation ($8x + 5y = 400$) from this result:
$(8x + 12y) - (8x + 5y) = 480 - 400$
$7y = 80$
$y = \frac{80}{7}$
Substitute the value of $y$ into the equation $2x + 3y = 120$:
$2x + 3\left(\frac{80}{7}\right) = 120$
$2x + \frac{240}{7} = 120$
$2x = 120 - \frac{240}{7} = \frac{120 \times 7 - 240}{7} = \frac{840 - 240}{7} = \frac{600}{7}$
$x = \frac{600}{7 \times 2} = \frac{300}{7}$
Point: ($\frac{300}{7}$, $\frac{80}{7}$). Since $x \geq 0$ and $y \geq 0$, this point is in the first quadrant and is feasible.
The vertices of the feasible region are (0, 0), (50, 0), ($\frac{300}{7}$, $\frac{80}{7}$), and (0, 40).
We evaluate the objective function $Z = x + y$ at each of these vertices:
| Vertex (x, y) | Value of Z = x + y |
| (0, 0) | $Z = 0 + 0 = 0$ |
| (50, 0) | $Z = 50 + 0 = 50$ |
| ($\frac{300}{7}$, $\frac{80}{7}$) | $Z = \frac{300}{7} + \frac{80}{7} = \frac{380}{7}$ |
| (0, 40) | $Z = 0 + 40 = 40$ |
Comparing the values of Z at the vertices:
$0$
$50$
$\frac{380}{7} \approx 54.2857$
$40$
The maximum value is $\frac{380}{7}$.
Conclusion:
The maximum distance that the man can travel is $\frac{380}{7}$ km (approximately 54.29 km).
This occurs when he travels $\frac{300}{7}$ km at 50 km/h and $\frac{80}{7}$ km at 80 km/h.
Question 21. Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
Answer:
Given:
Objective function to maximize: $Z = x + y$
Constraints:
$x + 4y \leq 8$
$2x + 3y \leq 12$
$3x + y \leq 9$
$x \geq 0$
$y \geq 0$
To Find:
The maximum value of Z subject to the given constraints.
Solution:
The given constraints define the feasible region. The constraints $x \geq 0$ and $y \geq 0$ restrict the region to the first quadrant.
We consider the boundary lines corresponding to the inequalities:
1. $x + 4y = 8$
2. $2x + 3y = 12$
3. $3x + y = 9$
We find the vertices (corner points) of the feasible region, which are the intersection points of these boundary lines within the first quadrant and satisfying all the inequalities.
The vertices are found by considering the intersection of pairs of boundary lines and the axes ($x=0, y=0$).
a) Intersection of $x=0$ and $y=0$: Point (0, 0).
b) Intersection of $y=0$ and $3x + y = 9$: Setting $y=0$, we get $3x = 9 \implies x = 3$. Point (3, 0). Check against $x+4y \leq 8$: $3+4(0)=3 \leq 8$ (True). Check against $2x+3y \leq 12$: $2(3)+3(0)=6 \leq 12$ (True). Feasible. Vertex: (3, 0).
c) Intersection of $x=0$ and $x + 4y = 8$: Setting $x=0$, we get $4y = 8 \implies y = 2$. Point (0, 2). Check against $2x+3y \leq 12$: $2(0)+3(2)=6 \leq 12$ (True). Check against $3x+y \leq 9$: $3(0)+2=2 \leq 9$ (True). Feasible. Vertex: (0, 2).
d) Intersection of $x + 4y = 8$ and $3x + y = 9$. From the second equation, $y = 9 - 3x$. Substituting into the first equation:
$x + 4(9 - 3x) = 8$
$x + 36 - 12x = 8$
$-11x = 8 - 36$
$-11x = -28 \implies x = \frac{28}{11}$
Substituting $x = \frac{28}{11}$ into $y = 9 - 3x$:
$y = 9 - 3\left(\frac{28}{11}\right) = 9 - \frac{84}{11} = \frac{99 - 84}{11} = \frac{15}{11}$
Point ($\frac{28}{11}$, $\frac{15}{11}$). Check against $2x+3y \leq 12$: $2\left(\frac{28}{11}\right) + 3\left(\frac{15}{11}\right) = \frac{56}{11} + \frac{45}{11} = \frac{101}{11}$. Since $\frac{101}{11} \approx 9.18 < 12$, this point is feasible. Vertex: ($\frac{28}{11}$, $\frac{15}{11}$).
e) Intersection of $2x+3y=12$ and $3x+y=9$. (As calculated in thought process, this point (15/7, 18/7) is not feasible with $x+4y \leq 8$).
f) Intersection of $x+4y=8$ and $2x+3y=12$. (As calculated in thought process, this point (24/5, 4/5) is not feasible with $3x+y \leq 9$).
The vertices of the feasible region are (0, 0), (3, 0), ($\frac{28}{11}$, $\frac{15}{11}$), and (0, 2).
Now, we evaluate the objective function $Z = x + y$ at each vertex:
| Vertex (x, y) | Value of Z = x + y |
| (0, 0) | $Z = 0 + 0 = 0$ |
| (3, 0) | $Z = 3 + 0 = 3$ |
| ($\frac{28}{11}$, $\frac{15}{11}$) | $Z = \frac{28}{11} + \frac{15}{11} = \frac{43}{11}$ |
| (0, 2) | $Z = 0 + 2 = 2$ |
Comparing the values of Z at the vertices: $0, 3, \frac{43}{11}, 2$.
Since $\frac{43}{11} = 3 + \frac{10}{11} \approx 3.91$, it is the largest value.
Conclusion:
The maximum value of Z is $\frac{43}{11}$, which occurs at the point ($\frac{28}{11}$, $\frac{15}{11}$).
Question 22. A manufacturer produces two Models of bikes - Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively.
How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
Answer:
Given:
Production time per unit:
Model X: 6 man-hours
Model Y: 10 man-hours
Total available man-hours per week: 450
Handling and Marketing cost per unit:
Model X: $\textsf{₹}2000$
Model Y: $\textsf{₹}1000$
Total funds available for these purposes per week: $\textsf{₹}80000$
Profit per unit:
Model X: $\textsf{₹}1000$
Model Y: $\textsf{₹}500$
To Find:
The number of bikes of each model (Model X and Model Y) that should be produced per week to maximize the profit, and the maximum profit.
Formulation as LPP:
Let $x$ be the number of units of Model X produced per week.
Let $y$ be the number of units of Model Y produced per week.
These are our decision variables.
The objective is to maximize the total profit.
The objective function to maximize is:
$Z = 1000x + 500y$
The constraints are based on the available man-hours and the available funds for handling and marketing.
Constraints:
1. Constraint on total man-hours:
Total man-hours used = (Man-hours for $x$ units of X) + (Man-hours for $y$ units of Y)
Total man-hours used = $6x + 10y$
Total available man-hours = 450
$6x + 10y \leq 450$
Dividing by 2, we get:
$3x + 5y \leq 225$
2. Constraint on handling and marketing funds:
Total cost for handling and marketing = (Cost for $x$ units of X) + (Cost for $y$ units of Y)
Total cost = $2000x + 1000y$
Total funds available = $\textsf{₹}80000$
$2000x + 1000y \leq 80000$
Dividing by 1000, we get:
$2x + y \leq 80$
Also, the number of units produced cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
Solving the LPP:
Maximize $Z = 1000x + 500y$
Subject to:
$3x + 5y \leq 225$
$2x + y \leq 80$
$x \geq 0, y \geq 0$
We find the vertices of the feasible region:
a) Intersection of $x=0$ and $y=0$: Point (0, 0).
b) Intersection of $y=0$ and $2x + y = 80$: Setting $y=0$, $2x=80 \implies x=40$. Point (40, 0). Check $3x+5y \leq 225$: $3(40)+5(0)=120 \leq 225$ (True). Feasible.
c) Intersection of $x=0$ and $3x + 5y = 225$: Setting $x=0$, $5y=225 \implies y=45$. Point (0, 45). Check $2x+y \leq 80$: $2(0)+45=45 \leq 80$ (True). Feasible.
d) Intersection of $3x + 5y = 225$ and $2x + y = 80$. From the second equation, $y = 80 - 2x$. Substitute into the first equation:
$3x + 5(80 - 2x) = 225$
$3x + 400 - 10x = 225$
$-7x = 225 - 400$
$-7x = -175 \implies x = \frac{175}{7} = 25$
Substitute $x=25$ into $y = 80 - 2x$:
$y = 80 - 2(25) = 80 - 50 = 30$
Point (25, 30).
The vertices of the feasible region are (0, 0), (40, 0), (25, 30), and (0, 45).
Evaluate the objective function $Z = 1000x + 500y$ at each vertex:
| Vertex (x, y) | Value of Z = 1000x + 500y |
| (0, 0) | $Z = 1000(0) + 500(0) = 0$ |
| (40, 0) | $Z = 1000(40) + 500(0) = 40000$ |
| (25, 30) | $Z = 1000(25) + 500(30) = 25000 + 15000 = 40000$ |
| (0, 45) | $Z = 1000(0) + 500(45) = 22500$ |
Comparing the values of Z at the vertices (0, 40000, 40000, 22500), the maximum value is 40000.
The maximum profit is $\textsf{₹}40000$, which occurs at two vertices: (40, 0) and (25, 30). This means any point on the line segment connecting (40, 0) and (25, 30) that is within the feasible region also yields the maximum profit. However, since the number of bikes must be integers, we look at the vertices.
Conclusion:
The maximum profit is $\textsf{₹}40000$.
This maximum profit can be achieved by producing either:
40 units of Model X and 0 units of Model Y, OR
25 units of Model X and 30 units of Model Y.
Question 23. In order to supplement daily diet, a person wishes to take some X and some wishes Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:
| Tablets | Iron | Calcium | Vitamin |
|---|---|---|---|
| X | 6 | 3 | 2 |
| Y | 2 | 3 | 4 |
The person needs at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligram of vitamins. The price of each tablet of X and Y is Rs 2 and Re 1 respectively. How many tablets of each should the person take inorder to satisfy the above requirement at the minimum cost?
Answer:
Given:
| Contents (mg/tablet) | Tablet X | Tablet Y | Minimum Daily Requirement (mg) |
| Iron | 6 | 2 | 18 |
| Calcium | 3 | 3 | 21 |
| Vitamin | 2 | 4 | 16 |
Cost per tablet:
Tablet X: $\textsf{₹}2$
Tablet Y: $\textsf{₹}1$
To Find:
The number of tablets of type X and type Y to take to minimize the total cost while satisfying the minimum daily requirement of nutrients.
Formulation as LPP:
Let $x$ be the number of tablets of type X taken.
Let $y$ be the number of tablets of type Y taken.
These are our decision variables. Since the number of tablets must be whole, this is ideally an Integer Programming problem, but we will solve it as a standard LPP and check the vertex solution.
The objective is to minimize the total cost.
The objective function to minimize is:
$Z = 2x + y$
The constraints are based on the minimum required amounts of iron, calcium, and vitamins.
Constraints:
1. Iron constraint:
$6x + 2y \geq 18$
Simplifying by dividing by 2:
$3x + y \geq 9$
2. Calcium constraint:
$3x + 3y \geq 21$
Simplifying by dividing by 3:
$x + y \geq 7$
3. Vitamin constraint:
$2x + 4y \geq 16$
Simplifying by dividing by 2:
$x + 2y \geq 8$
Also, the number of tablets cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
Solving the LPP:
Minimize $Z = 2x + y$
Subject to:
$3x + y \geq 9$
$x + y \geq 7$
$x + 2y \geq 8$
$x \geq 0, y \geq 0$
The feasible region is in the first quadrant ($x \geq 0, y \geq 0$) and is the area above or on the lines $3x+y=9$, $x+y=7$, and $x+2y=8$.
We find the vertices (corner points) of this feasible region:
a) Intersection of $x=0$ and $3x+y=9$: $(0, 9)$. Check $0+9 \geq 7$ (True), $0+2(9)=18 \geq 8$ (True). Vertex: (0, 9).
b) Intersection of $y=0$ and $x+2y=8$: $(8, 0)$. Check $3(8)+0=24 \geq 9$ (True), $8+0 \geq 7$ (True). Vertex: (8, 0).
c) Intersection of $3x+y=9$ and $x+y=7$:
$3x + y = 9$
... (i)
$x + y = 7$
... (ii)
Subtract (ii) from (i): $(3x+y) - (x+y) = 9-7 \implies 2x = 2 \implies x=1$.
Substitute $x=1$ into $x+y=7$: $1+y=7 \implies y=6$. Point (1, 6).
Check $x+2y \geq 8$: $1+2(6) = 1+12 = 13 \geq 8$ (True). Feasible. Vertex: (1, 6).
d) Intersection of $x+y=7$ and $x+2y=8$:
$x + y = 7$
... (iii)
$x + 2y = 8$
... (iv)
Subtract (iii) from (iv): $(x+2y) - (x+y) = 8-7 \implies y = 1$.
Substitute $y=1$ into $x+y=7$: $x+1=7 \implies x=6$. Point (6, 1).
Check $3x+y \geq 9$: $3(6)+1 = 18+1 = 19 \geq 9$ (True). Feasible. Vertex: (6, 1).
e) Intersection of $3x+y=9$ and $x+2y=8$. (As determined in thought process, this point (2, 3) is not feasible with $x+y \geq 7$).
The vertices of the feasible region are (0, 9), (1, 6), (6, 1), and (8, 0).
We evaluate the objective function $Z = 2x + y$ at each vertex:
| Vertex (x, y) | Value of Z = 2x + y |
| (0, 9) | $Z = 2(0) + 9 = 9$ |
| (1, 6) | $Z = 2(1) + 6 = 2 + 6 = 8$ |
| (6, 1) | $Z = 2(6) + 1 = 12 + 1 = 13$ |
| (8, 0) | $Z = 2(8) + 0 = 16 + 0 = 16$ |
Comparing the values of Z at the vertices (9, 8, 13, 16), the minimum value is 8.
This minimum cost occurs at the vertex (1, 6).
Since the coordinates of the optimal vertex are integers, the integer solution is the same as the real solution.
Conclusion:
To satisfy the requirements at the minimum cost, the person should take 1 tablet of type X and 6 tablets of type Y.
The minimum cost will be $\textsf{₹}8$.
Question 24. A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate tominimise the operating costs and still meet the demand.
Answer:
Given:
Minimum required calculators:
Model A: 6400
Model B: 4000
Model C: 4800
Production capacity per day:
Factory I: 50 (A), 50 (B), 30 (C)
Factory II: 40 (A), 20 (B), 40 (C)
Operating cost per day:
Factory I: $\textsf{₹}12000$
Factory II: $\textsf{₹}15000$
Objective: Minimise the total operating cost.
To Find:
The number of days each factory should operate to meet the demand at the minimum operating cost, and the minimum cost.
Formulation as LPP:
Let $x$ be the number of days Factory I operates.
Let $y$ be the number of days Factory II operates.
These are our decision variables.
The objective is to minimize the total operating cost.
The objective function to minimize is:
$Z = 12000x + 15000y$
The constraints are based on meeting the minimum demand for each model.
Constraints:
1. Constraint for Model A demand:
Total Model A produced = (Production from Factory I) + (Production from Factory II)
Total Model A produced = $50x + 40y$
Minimum required = 6400
$50x + 40y \geq 6400$
Dividing by 10:
$5x + 4y \geq 640$
2. Constraint for Model B demand:
Total Model B produced = $50x + 20y$
Minimum required = 4000
$50x + 20y \geq 4000$
Dividing by 10:
$5x + 2y \geq 400$
3. Constraint for Model C demand:
Total Model C produced = $30x + 40y$
Minimum required = 4800
$30x + 40y \geq 4800$
Dividing by 10:
$3x + 4y \geq 480$
Also, the number of days operated cannot be negative.
Non-negativity constraints:
$x \geq 0$
$y \geq 0$
Since the number of days must be integers, $x$ and $y$ are also restricted to be integers. We will solve as a standard LPP and check the optimal vertex.
Solving the LPP:
Minimize $Z = 12000x + 15000y$
Subject to:
$5x + 4y \geq 640$
$5x + 2y \geq 400$
$3x + 4y \geq 480$
$x \geq 0, y \geq 0$
We find the vertices of the feasible region, which is the area in the first quadrant satisfying all '$\geq$' inequalities. The vertices are the intersection points of the boundary lines that define the boundaries of this feasible region.
Boundary lines are $5x + 4y = 640$, $5x + 2y = 400$, $3x + 4y = 480$, $x=0$, and $y=0$.
The vertices of the feasible region are:
a) Intersection of $x=0$ and $5x + 4y = 640$ is (0, 160). Check other constraints: $5(0)+2(160)=320 \geq 400$ (False). Not a vertex of the feasible region.
b) Intersection of $x=0$ and $3x + 4y = 480$ is (0, 120). Check other constraints: $5(0)+2(120)=240 \geq 400$ (False). Not a vertex of the feasible region.
c) Intersection of $x=0$ and $5x + 2y = 400$ is (0, 200). Check other constraints: $5(0)+4(200)=800 \geq 640$ (True), $3(0)+4(200)=800 \geq 480$ (True). Vertex: (0, 200).
d) Intersection of $y=0$ and $5x + 2y = 400$ is (80, 0). Check other constraints: $5(80)+4(0)=400 \geq 640$ (False). Not a vertex of the feasible region.
e) Intersection of $y=0$ and $3x + 4y = 480$ is (160, 0). Check other constraints: $5(160)+4(0)=800 \geq 640$ (True), $5(160)+2(0)=800 \geq 400$ (True). Vertex: (160, 0).
f) Intersection of $5x + 4y = 640$ and $5x + 2y = 400$. Subtracting the second from the first: $2y = 240 \implies y = 120$. Substituting into $5x+2y=400$: $5x + 2(120) = 400 \implies 5x + 240 = 400 \implies 5x = 160 \implies x = 32$. Point (32, 120). Check third constraint: $3(32)+4(120) = 96 + 480 = 576 \geq 480$ (True). Vertex: (32, 120).
g) Intersection of $5x + 4y = 640$ and $3x + 4y = 480$. Subtracting the second from the first: $2x = 160 \implies x = 80$. Substituting into $3x+4y=480$: $3(80)+4y=480 \implies 240+4y=480 \implies 4y=240 \implies y=60$. Point (80, 60). Check second constraint: $5(80)+2(60)=400+120=520 \geq 400$ (True). Vertex: (80, 60).
h) Intersection of $5x + 2y = 400$ and $3x + 4y = 480$. (As determined in thought process, this point is not in the feasible region).
The vertices of the feasible region are (0, 200), (32, 120), (80, 60), and (160, 0).
We evaluate the objective function $Z = 12000x + 15000y$ at each vertex:
| Vertex (x, y) | Value of Z = 12000x + 15000y |
| (0, 200) | $Z = 12000(0) + 15000(200) = 0 + 3000000 = 3,000,000$ |
| (32, 120) | $Z = 12000(32) + 15000(120) = 384000 + 1800000 = 2,184,000$ |
| (80, 60) | $Z = 12000(80) + 15000(60) = 960000 + 900000 = 1,860,000$ |
| (160, 0) | $Z = 12000(160) + 15000(0) = 1920000 + 0 = 1,920,000$ |
Comparing the values of Z at the vertices (3,000,000, 2,184,000, 1,860,000, 1,920,000), the minimum value is 1,860,000.
The feasible region is unbounded, but since the objective function involves minimizing with positive coefficients and the constraints are all '$\geq$' type, the minimum value exists and occurs at a corner point.
The optimal vertex is (80, 60), which consists of integer values, satisfying the implicit requirement that the number of days must be a whole number.
Conclusion:
To minimize the operating costs and still meet the demand, Factory I should operate for 80 days and Factory II should operate for 60 days.
The minimum operating cost will be $\textsf{₹}1,860,000$.
Question 25. Maximise and Minimise Z = 3x – 4y
subject to
x – 2y ≤ 0
– 3x + y ≤ 4
x – y ≤ 6
x, y ≥ 0
Answer:
Given:
Objective function: Maximize and Minimize $Z = 3x – 4y$
Constraints:
$x – 2y \leq 0$
$- 3x + y \leq 4$
$x – y \leq 6$
$x \geq 0$
$y \geq 0$
To Find:
The maximum and minimum values of Z subject to the given constraints.
Solution:
We first identify the feasible region defined by the given constraints. The constraints $x \geq 0$ and $y \geq 0$ mean the feasible region lies in the first quadrant.
The boundary lines for the other constraints are:
1. $x – 2y = 0 \implies y = \frac{1}{2}x$
2. $- 3x + y = 4 \implies y = 3x + 4$
3. $x – y = 6 \implies y = x – 6$
We find the vertices (corner points) of the feasible region by finding the intersection points of these boundary lines within the first quadrant that satisfy all the inequalities.
The vertices of the feasible region are found by intersecting the boundary lines:
a) Intersection of $x=0$ and $y=0$: (0, 0). This point satisfies all constraints ($0 \leq 0, 0 \leq 4, 0 \leq 6, 0 \geq 0, 0 \geq 0$). Vertex: (0, 0).
b) Intersection of $x=0$ and $y=3x+4$: Setting $x=0$ in $y=3x+4$ gives $y=4$. Point (0, 4). Check other constraints: $0-2(4)=-8 \leq 0$ (T), $-3(0)+4=4 \leq 4$ (T), $0-4=-4 \leq 6$ (T), $0 \geq 0, 4 \geq 0$ (T). Vertex: (0, 4).
c) Intersection of $y=x/2$ and $y=x-6$: Substitute $y=x/2$ into $y=x-6$: $\frac{x}{2} = x - 6 \implies x = 2x - 12 \implies x = 12$. Then $y = 12/2 = 6$. Point (12, 6). Check other constraints: $-3(12)+6 = -36+6 = -30 \leq 4$ (T), $12-6 = 6 \leq 6$ (T), $12 \geq 0, 6 \geq 0$ (T). Vertex: (12, 6).
d) Intersection of $y=3x+4$ and $x=12$: Setting $x=12$ in $y=3x+4$ gives $y=3(12)+4 = 36+4 = 40$. Point (12, 40). Check other constraints: $12-2(40)=12-80=-68 \leq 0$ (T), $-3(12)+40=-36+40=4 \leq 4$ (T), $12-40=-28 \leq 6$ (T), $12 \geq 0, 40 \geq 0$ (T). Vertex: (12, 40).
Other intersections (e.g., $y=x/2$ and $y=3x+4$, $y=3x+4$ and $y=x-6$, $y=x-6$ and $y=0$) do not result in vertices of the feasible region in the first quadrant satisfying all inequalities.
The feasible region is a bounded polygon with vertices (0, 0), (0, 4), (12, 40), and (12, 6).
We evaluate the objective function $Z = 3x - 4y$ at each vertex:
| Vertex (x, y) | Value of Z = 3x – 4y |
| (0, 0) | $Z = 3(0) - 4(0) = 0$ |
| (0, 4) | $Z = 3(0) - 4(4) = -16$ |
| (12, 6) | $Z = 3(12) - 4(6) = 36 - 24 = 12$ |
| (12, 40) | $Z = 3(12) - 4(40) = 36 - 160 = -124$ |
Comparing the values of Z at the vertices (0, -16, 12, -124), we find the minimum and maximum values.
The minimum value is -124.
The maximum value is 12.
Conclusion:
The minimum value of Z is -124, which occurs at the vertex (12, 40).
The maximum value of Z is 12, which occurs at the vertex (12, 6).
Question 26 to 34 (Multiple Choice Questions)
Choose the correct answer from the given four options in each of the Exercises 26 to 34.
Question 26. The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in Column A and Column B
Column A
Maximum of Z
Column B
325
(A) The quantity in column A is greater
(B) The quantity in column B is greater
(C) The two quantities are equal
(D) The relationship can not be determined on the basis of the information supplied
Answer:
Given:
The corner points of the feasible region are (0, 0), (0, 40), (20, 40), (60, 20), and (60, 0).
Objective Function:
$Z = 4x + 3y$
To Find:
The maximum value of Z and compare it with 325.
Solution:
We evaluate the objective function $Z = 4x + 3y$ at each of the given corner points.
| Corner Point (x, y) | Value of Z = 4x + 3y |
| (0, 0) | $Z = 4(0) + 3(0) = 0$ |
| (0, 40) | $Z = 4(0) + 3(40) = 0 + 120 = 120$ |
| (20, 40) | $Z = 4(20) + 3(40) = 80 + 120 = 200$ |
| (60, 20) | $Z = 4(60) + 3(20) = 240 + 60 = 300$ |
| (60, 0) | $Z = 4(60) + 3(0) = 240 + 0 = 240$ |
The values of Z at the corner points are 0, 120, 200, 300, and 240.
The maximum value of Z is the largest among these values, which is 300.
So, the quantity in Column A (Maximum of Z) is 300.
Comparison:
Column A = Maximum of Z = 300
Column B = 325
Comparing Column A and Column B: $300 < 325$
The quantity in Column B is greater than the quantity in Column A.
Conclusion:
The quantity in Column B is greater.
Therefore, the correct option is (B) The quantity in column B is greater.
Question 27. The feasible solution for a LPP is shown in Fig. 12.12. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at
(A) (0, 0)
(B) (0, 8)
(C) (5, 0)
(D) (4, 10)
Answer:
Given:
The feasible region is shown in the figure.
The corner points of the feasible region, as visible from the figure, are (0, 0), (5, 0), (4, 10), and (0, 8).
Objective Function:
$Z = 3x - 4y$
To Find:
The corner point where the minimum value of Z occurs.
Solution:
We evaluate the objective function $Z = 3x - 4y$ at each of the corner points of the feasible region.
| Corner Point (x, y) | Value of Z = 3x - 4y |
| (0, 0) | $Z = 3(0) - 4(0) = 0 - 0 = 0$ |
| (5, 0) | $Z = 3(5) - 4(0) = 15 - 0 = 15$ |
| (4, 10) | $Z = 3(4) - 4(10) = 12 - 40 = -28$ |
| (0, 8) | $Z = 3(0) - 4(8) = 0 - 32 = -32$ |
The values of Z at the corner points are 0, 15, -28, and -32.
The minimum value of Z is the smallest among these values, which is -32.
This minimum value of Z occurs at the corner point (0, 8).
Conclusion:
The minimum of Z occurs at the point (0, 8).
Therefore, the correct option is (B) (0, 8).
Question 28. Refer to Exercise 27. Maximum of Z occurs at
(A) (5, 0)
(B) (6, 5)
(C) (6, 8)
(D) (4, 10)
Answer:
Given:
This question refers to Exercise 27. From the figure in Exercise 27, the corner points of the feasible region are (0, 0), (5, 0), (4, 10), and (0, 8).
Objective Function:
From Exercise 27, the objective function is $Z = 3x - 4y$.
To Find:
The corner point where the maximum value of Z occurs.
Solution:
We evaluate the objective function $Z = 3x - 4y$ at each of the corner points of the feasible region, as determined in Exercise 27.
| Corner Point (x, y) | Value of Z = 3x - 4y |
| (0, 0) | $Z = 3(0) - 4(0) = 0 - 0 = 0$ |
| (5, 0) | $Z = 3(5) - 4(0) = 15 - 0 = 15$ |
| (4, 10) | $Z = 3(4) - 4(10) = 12 - 40 = -28$ |
| (0, 8) | $Z = 3(0) - 4(8) = 0 - 32 = -32$ |
The values of Z at the corner points are 0, 15, -28, and -32.
The maximum value of Z is the largest among these values, which is 15.
This maximum value of Z occurs at the corner point (5, 0).
Conclusion:
The maximum of Z occurs at the point (5, 0).
Therefore, the correct option is (A) (5, 0).
Question 29. Refer to Exercise 27. (Maximum value of Z + Minimum value of Z) is equal to
(A) 13
(B) 1
(C) – 13
(D) – 17
Answer:
Given:
This question refers to Exercise 27.
From the solution of Exercise 27, the minimum value of the objective function $Z = 3x - 4y$ in the given feasible region is -32.
From the solution of Exercise 28, the maximum value of the objective function $Z = 3x - 4y$ in the given feasible region is 15.
To Find:
The sum of the maximum and minimum values of Z.
Solution:
Minimum value of Z = -32
Maximum value of Z = 15
We need to calculate (Maximum value of Z + Minimum value of Z).
Sum = Maximum value of Z + Minimum value of Z
Sum = $15 + (-32)$
Sum = $15 - 32$
Sum = $-17$
Conclusion:
The sum of the maximum and minimum values of Z is -17.
Therefore, the correct option is (D) – 17.
Question 30. The feasible region for an LPP is shown in the Fig. 12.13. Let F = 3x – 4y be the objective function. Maximum value of F is.
(A) 0
(B) 8
(C) 12
(D) – 18
Answer:
Given:
The feasible region is shown in the figure. The corner points of the feasible region, as identified from the figure, are (8, 0), (12, 0), (6, 5), and (0, 8).
Objective Function:
$F = 3x - 4y$
To Find:
The maximum value of the objective function F in the given feasible region.
Solution:
We evaluate the objective function $F = 3x - 4y$ at each of the corner points of the feasible region.
| Corner Point (x, y) | Value of F = 3x - 4y |
| (8, 0) | $F = 3(8) - 4(0) = 24 - 0 = 24$ |
| (12, 0) | $F = 3(12) - 4(0) = 36 - 0 = 36$ |
| (6, 5) | $F = 3(6) - 4(5) = 18 - 20 = -2$ |
| (0, 8) | $F = 3(0) - 4(8) = 0 - 32 = -32$ |
The values of F at the corner points are 24, 36, -2, and -32.
The maximum value of F is the largest among these values, which is 36.
Conclusion:
The maximum value of F is 36.
(Note: The calculated maximum value 36 is not among the given options. Based on the provided problem statement and figure, the maximum value is 36).
Question 31. Refer to Exercise 30. Minimum value of F is
(A) 0
(B) – 16
(C) 12
(D) does not exist
Answer:
Given:
This question refers to Exercise 30. From the figure in Exercise 30, the corner points of the feasible region are (8, 0), (12, 0), (6, 5), and (0, 8).
Objective Function:
From Exercise 30, the objective function is $F = 3x - 4y$.
To Find:
The minimum value of the objective function F in the given feasible region.
Solution:
We evaluate the objective function $F = 3x - 4y$ at each of the corner points of the feasible region.
| Corner Point (x, y) | Value of F = 3x - 4y |
| (8, 0) | $F = 3(8) - 4(0) = 24 - 0 = 24$ |
| (12, 0) | $F = 3(12) - 4(0) = 36 - 0 = 36$ |
| (6, 5) | $F = 3(6) - 4(5) = 18 - 20 = -2$ |
| (0, 8) | $F = 3(0) - 4(8) = 0 - 32 = -32$ |
The values of F at the corner points are 24, 36, -2, and -32.
The minimum value of F is the smallest among these values, which is -32.
Conclusion:
The minimum value of F is -32.
Upon comparing this value with the given options, it is observed that -32 is not among the options (A) 0, (B) – 16, (C) 12, (D) does not exist. Since the feasible region is bounded, a minimum value must exist.
Based on the provided figure and objective function, the minimum value calculated is -32.
Question 32. Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5).
Let F = 4x + 6y be the objective function.
The Minimum value of F occurs at
(A) (0, 2) only
(B) (3, 0) only
(C) the mid point of the line sgment joining the points (0, 2) and (3, 0) only
(D) any point on the line segment joining the points (0, 2) and (3, 0).
Answer:
Given:
The corner points of the feasible region are (0, 2), (3, 0), (6, 0), (6, 8), and (0, 5).
Objective Function:
$F = 4x + 6y$
To Find:
The point(s) where the minimum value of F occurs.
Solution:
We evaluate the objective function $F = 4x + 6y$ at each of the given corner points of the feasible region.
| Corner Point (x, y) | Value of F = 4x + 6y |
| (0, 2) | $F = 4(0) + 6(2) = 0 + 12 = 12$ |
| (3, 0) | $F = 4(3) + 6(0) = 12 + 0 = 12$ |
| (6, 0) | $F = 4(6) + 6(0) = 24 + 0 = 24$ |
| (6, 8) | $F = 4(6) + 6(8) = 24 + 48 = 72$ |
| (0, 5) | $F = 4(0) + 6(5) = 0 + 30 = 30$ |
The values of F at the corner points are 12, 12, 24, 72, and 30.
The minimum value of F is the smallest among these values, which is 12.
This minimum value occurs at two distinct corner points: (0, 2) and (3, 0).
According to the fundamental theorem of linear programming, if the optimal value (maximum or minimum) of the objective function occurs at two corner points of the feasible region, then it occurs at every point on the line segment joining these two points.
Conclusion:
The minimum value of F occurs at any point on the line segment joining the points (0, 2) and (3, 0).
Therefore, the correct option is (D) any point on the line segment joining the points (0, 2) and (3, 0).
Question 33. Refer to Exercise 32, Maximum of F – Minimum of F =
(A) 60
(B) 48
(C) 42
(D) 18
Answer:
Given:
This question refers to Exercise 32. From the solution to Exercise 32, we evaluated the objective function $F = 4x + 6y$ at the corner points of the feasible region.
Values of F at Corner Points (from Exercise 32):
F(0, 2) = 12
F(3, 0) = 12
F(6, 0) = 24
F(6, 8) = 72
F(0, 5) = 30
Maximum and Minimum Values of F:
From the values calculated above:
The minimum value of F is 12.
The maximum value of F is 72.
To Find:
Maximum of F - Minimum of F.
Solution:
Maximum of F - Minimum of F = $72 - 12$
Maximum of F - Minimum of F = $60$
Conclusion:
The difference between the maximum and minimum values of F is 60.
Therefore, the correct option is (A) 60.
Question 34. Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
(A) p = 2q
(B) $p = \frac{q}{2}$
(C) p = 3q
(D) p = q
Answer:
Given:
The corner points of the feasible region are (0, 3), (1, 1), and (3, 0).
The objective function is $Z = px + qy$, where $p > 0$ and $q > 0$.
The minimum value of Z occurs at the points (3, 0) and (1, 1).
To Find:
The condition on p and q for the minimum of Z to occur at both (3, 0) and (1, 1).
Solution:
If the minimum value of the objective function occurs at two corner points of the feasible region, then the minimum value of the objective function is the same at these two points. This also implies that the minimum value occurs at every point on the line segment joining these two points.
Given that the minimum of Z occurs at (3, 0) and (1, 1), the value of Z at (3, 0) must be equal to the value of Z at (1, 1).
Let's evaluate the objective function $Z = px + qy$ at these two points:
Value of Z at (3, 0):
$Z(3, 0) = p(3) + q(0) = 3p$
Value of Z at (1, 1):
$Z(1, 1) = p(1) + q(1) = p + q$
Since the minimum occurs at both points, we have:
Z(3, 0) = Z(1, 1)
$3p = p + q$
Now, we solve for the relationship between p and q:
$3p - p = q$
$2p = q$
This relationship can also be written as $p = \frac{q}{2}$.
Let's verify if this value is indeed the minimum by evaluating Z at the remaining corner point (0, 3).
Value of Z at (0, 3):
$Z(0, 3) = p(0) + q(3) = 3q$
Substitute $q = 2p$ (since $p, q > 0$):
$Z(0, 3) = 3(2p) = 6p$
Now compare the values:
$Z(3, 0) = 3p$
$Z(1, 1) = p + q = p + 2p = 3p$
$Z(0, 3) = 6p$
Since $p > 0$, we have $3p < 6p$. Thus, $3p$ is indeed the minimum value among the corner points when $q = 2p$.
Conclusion:
The condition on p and q for the minimum of Z to occur at (3, 0) and (1, 1) is $2p = q$ or $p = \frac{q}{2}$.
Comparing with the given options, the correct option is (B) $p = \frac{q}{2}$.
Question 35 to 41 (Fill in the Blanks)
Fill in the blanks in each of the Exercises 35 to 41.
Question 35. In a LPP, the linear inequalities or restrictions on the variables are called _________.
Answer:
Answer: constraints
Explanation:
In a Linear Programming Problem (LPP), the goal is to optimize (maximize or minimize) a linear objective function subject to certain limitations or restrictions.
These restrictions are expressed in the form of linear inequalities or sometimes linear equations involving the decision variables.
These linear inequalities or equations that limit the values of the variables are formally called constraints.
For example, if you are producing two types of goods, X and Y, and have limited raw materials and labor hours, the inequalities representing these limitations (e.g., amount of raw material used $\le$ total raw material available) are the constraints.
The set of all points satisfying all the constraints simultaneously forms the feasible region, which represents all possible valid solutions to the problem.
Common examples of constraints include resource constraints (like material, labor, machine time), demand constraints, and non-negativity constraints (variables like quantity produced cannot be negative, i.e., $x \ge 0, y \ge 0$).
Question 36. In a LPP, the objective function is always _________
Answer:
Answer: linear
Explanation:
A Linear Programming Problem (LPP) is a mathematical method for determining a way to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships.
The term "Linear" in Linear Programming Problem specifically refers to the fact that both the objective function and the constraints are expressed as linear functions of the decision variables.
The objective function is the function that you want to maximize or minimize. In an LPP, this function is always a linear combination of the variables.
For example, if the variables are $x$ and $y$, a linear objective function would look like $Z = ax + by$, where $a$ and $b$ are constants.
Functions like $Z = x^2 + y$ or $Z = xy$ are not linear, and therefore, problems involving such functions as the objective function are not considered LPPs in the standard sense.
Question 37. If the feasible region for a LPP is _________, then the optimal value of the objective function Z = ax + by may or may not exist.
Answer:
Answer: unbounded
Explanation:
In a Linear Programming Problem (LPP), the feasible region is the set of all points that satisfy all the constraints. The optimal solution (maximum or minimum value of the objective function) is usually found at one of the corner points of the feasible region.
If the feasible region is bounded, it means it can be enclosed within a finite region. In this case, the objective function $Z = ax + by$ will always attain both a maximum and a minimum value at one or more of the corner points.
However, if the feasible region is unbounded, it extends infinitely in one or more directions. In such a case, the objective function $Z = ax + by$:
1. May have a minimum value but no maximum value.
2. May have a maximum value but no minimum value.
3. May have neither a maximum nor a minimum value.
For example, if the feasible region is the first quadrant ($x \ge 0, y \ge 0$) and the objective function is $Z = x + y$, then Z can increase indefinitely as x and y increase, so there is no maximum. The minimum value occurs at (0, 0), which is 0.
The question states that the optimal value (maximum or minimum) "may or may not exist", which is characteristic of an unbounded feasible region.
Question 38. In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same _________ value.
Answer:
Answer: maximum
Explanation:
In a Linear Programming Problem (LPP), the feasible region is a convex set, and the optimal value (maximum or minimum) of the linear objective function $Z = ax + by$ occurs at one or more corner points of the feasible region.
A fundamental theorem of linear programming states that if the optimal value of the objective function is attained at two distinct corner points, it is also attained at every point on the line segment joining these two points.
This means if the maximum value of Z is the same at corner point A and corner point B, then any point $(x, y)$ lying on the line segment AB will also result in the same maximum value for the objective function $Z = ax + by$.
Therefore, every point on the line segment joining the two points gives the same maximum value.
Question 39. A feasible region of a system of linear inequalities is said to be _________ if it can be enclosed within a circle.
Answer:
Answer: bounded
Explanation:
In the context of Linear Programming Problems (LPPs), the feasible region is the set of all points that satisfy all the given linear constraints.
A feasible region is classified as either bounded or unbounded.
A feasible region is said to be bounded if it is possible to draw a circle (of sufficiently large radius) such that the entire feasible region lies within that circle. This means the feasible region does not extend infinitely in any direction.
Conversely, a feasible region is said to be unbounded if it cannot be enclosed within any finite circle. This occurs when the feasible region extends infinitely in one or more directions.
The description "can be enclosed within a circle" is the defining characteristic of a bounded feasible region.
Question 40. A corner point of a feasible region is a point in the region which is the _________ of two boundary lines.
Answer:
Answer: intersection
Explanation:
In a Linear Programming Problem (LPP), the feasible region is defined by a system of linear inequalities (constraints).
Each inequality corresponds to a half-plane, and the feasible region is the intersection of all these half-planes.
The boundary of each half-plane is a straight line, which is obtained by replacing the inequality sign with an equality sign.
A corner point (also known as a vertex) of the feasible region is a point where two or more of these boundary lines intersect.
These intersection points lie within or on the boundary of the feasible region.
According to the corner point theorem, the optimal solution (maximum or minimum value) of the objective function, if it exists, will occur at one of these corner points.
Thus, a corner point is specifically the intersection of two boundary lines of the feasible region.
Question 41. The feasible region for an LPP is always a _________ polygon.
Answer:
Answer: convex
Explanation:
In a Linear Programming Problem (LPP), the feasible region is defined by a system of linear inequalities.
Each linear inequality in two variables, say $ax + by \le c$ or $ax + by \ge c$, represents a half-plane in the plane. A half-plane is a region on one side of a straight line $ax + by = c$.
A key property of a half-plane is that it is a convex set. A set is convex if, for any two points within the set, the entire line segment connecting those two points also lies within the set.
The feasible region of an LPP is the set of points that satisfy all the linear constraints simultaneously. In other words, it is the intersection of all the half-planes defined by the constraints.
A fundamental property of convex sets is that the intersection of any number of convex sets is also a convex set.
Since the feasible region is the intersection of half-planes (which are convex sets), the feasible region itself is always a convex set.
If the feasible region is bounded and non-empty, it forms a polygon. Because it is a convex set, this polygon will always be a convex polygon.
A convex polygon has the property that for any two points inside or on the boundary of the polygon, the line segment connecting them lies entirely within or on the boundary of the polygon.
Question 42 to 45 (True or False)
State whether the statements in Exercises 42 to 45 are True or False.
Question 42. If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
Answer:
Answer: True
Explanation:
This statement is correct. When the feasible region of a Linear Programming Problem (LPP) is unbounded, the objective function does not necessarily attain an optimal value (maximum or minimum).
While an optimal value might exist (e.g., a minimum value may exist but no maximum, or vice versa), it is not guaranteed that both a maximum and a minimum value will exist, or even that one of them will exist, depending on the direction in which the objective function increases or decreases relative to the unbounded part of the feasible region.
For example, if the feasible region is $x \ge 0, y \ge 0$ (unbounded) and the objective function is $Z = x + y$, there is no maximum value as Z can increase indefinitely. However, the minimum value is 0 at (0, 0).
If the objective function was $Z = -x - y$ over the same feasible region, there would be no minimum value, but the maximum value would be 0 at (0, 0).
Since the optimal value (maximum or minimum) is not always guaranteed to exist in an unbounded feasible region, the statement that it "may or may not exist" is true.
Question 43. Maximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
Answer:
Answer: False
Explanation:
This statement is incorrect.
While it is true that if the maximum value of the objective function exists in a Linear Programming Problem (LPP) with a bounded feasible region, it will occur at a corner point, it does not necessarily occur at only one corner point.
According to the fundamental theorem of linear programming, if the optimal value (maximum or minimum) of the objective function occurs at two distinct corner points of the feasible region, then it occurs at every point on the line segment joining these two points.
This means the maximum value can occur at:
1. Exactly one corner point.
2. At two (or more) corner points and every point on the line segment(s) connecting them.
Therefore, the statement that the maximum value always occurs at only one corner point is false, as it can occur at infinitely many points if it occurs at two distinct corner points.
Question 44. In a LPP, the minimum value of the objective function Z = ax + by is always 0 if origin is one of the corner point of the feasible region.
Answer:
Answer: False
Explanation:
This statement is incorrect.
If the origin (0, 0) is a corner point of the feasible region, the value of the objective function $Z = ax + by$ at the origin is:
$Z(0, 0) = a(0) + b(0) = 0$
While the objective function has a value of 0 at the origin, this value is not necessarily the minimum value of Z over the entire feasible region.
The minimum value of the objective function occurs at one or more corner points of the feasible region. If there are other corner points where the objective function takes a negative value, then that negative value would be the minimum, which is less than 0.
For example, consider the objective function $Z = x - y$ and a feasible region with corner points (0, 0), (5, 0), and (0, 3). The origin (0, 0) is a corner point.
Evaluate Z at the corner points:
$Z(0, 0) = 0 - 0 = 0$
$Z(5, 0) = 5 - 0 = 5$
$Z(0, 3) = 0 - 3 = -3$
In this example, the minimum value of Z is -3, which occurs at the point (0, 3), even though the origin (0, 0) is a corner point and Z(0, 0) = 0.
Therefore, the minimum value of the objective function is not always 0 just because the origin is a corner point. It depends on the coefficients $a$ and $b$ and the location of the other corner points of the feasible region.
Question 45. In a LPP, the maximum value of the objective function Z = ax + by is always finite.
Answer:
Answer: False
Explanation:
This statement is incorrect.
In a Linear Programming Problem (LPP), the maximum value of the objective function $Z = ax + by$ is not always finite.
The existence and finiteness of the maximum value depend on the nature of the feasible region:
1. If the feasible region is bounded (can be enclosed within a circle), then the objective function will always attain both a maximum and a minimum value, and these values will be finite.
2. If the feasible region is unbounded (extends infinitely in at least one direction), the objective function may or may not have a maximum value. If the objective function increases indefinitely within the feasible region, then its maximum value does not exist (or is infinite).
For example, consider the LPP:
Maximize $Z = x + y$
Subject to the constraints:
$x \ge 0$
$y \ge 0$
The feasible region is the entire first quadrant, which is an unbounded region. As $x$ and $y$ increase, the value of $Z = x + y$ also increases without limit. Therefore, the maximum value of Z does not exist (it is not finite).
Since there exist LPPs with unbounded feasible regions where the maximum value of the objective function is not finite, the statement "the maximum value of the objective function Z = ax + by is always finite" is false.

